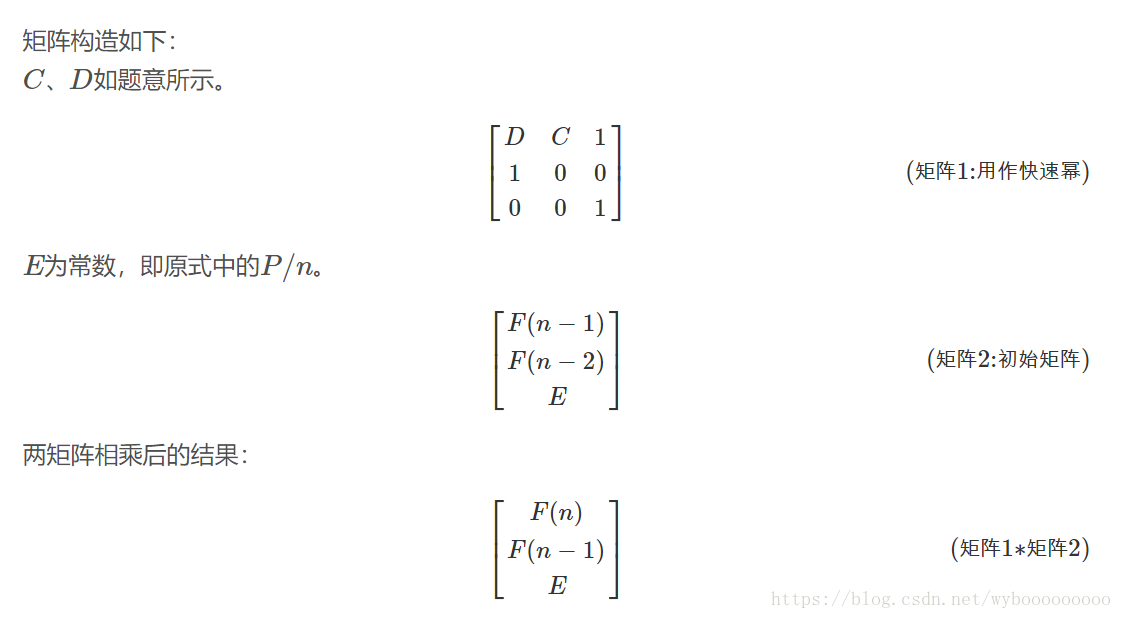hdu 6395Sequence【矩阵快速幂】【分块】
Sequence
Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 262144/262144 K (Java/Others)
Total Submission(s): 1951 Accepted Submission(s): 750
Problem Description
Let us define a sequence as below
⎧⎩⎨⎪⎪⎪⎪⎪⎪F1F2Fn===ABC⋅Fn−2+D⋅Fn−1+⌊Pn⌋
Your job is simple, for each task, you should output Fn module 109+7.
Input
The first line has only one integer T, indicates the number of tasks.
Then, for the next T lines, each line consists of 6 integers, A , B, C, D, P, n.
1≤T≤200≤A,B,C,D≤1091≤P,n≤109
Sample Input
2 3 3 2 1 3 5 3 2 2 2 1 4
Sample Output
36 24
Source
2018 Multi-University Training Contest 7
Recommend
chendu | We have carefully selected several similar problems for you: 6408 6407 6406 6405 6404
学习了一个新的递推求数的方法
通过构造矩阵 用矩阵递推 用矩阵快速幂优化 可以用来求一个随机的很大的数的值
矩阵快速幂的写法 O(logn)

这道题还有一点特别的是 后面的常数项是会变化的 但是他是分段的
所以就分块的来求 因为要知道乘的次数所以每次要求一下这个区间有多少个数
c++TLE g++AC
#include<iostream>
#include<stdio.h>
#include<string.h>
#include<algorithm>
#include<stack>
#define inf 1e18
using namespace std;
long long t, a, b, c, d, p, n;
const int mod = 1e9 + 7;
struct mat{
long long m[3][3];
mat(){
memset(m, 0, sizeof(m));
}
void init()
{
memset(m, 0, sizeof(m));
for(int i = 0; i < 3; i++){
m[i][i] = 1;
}
}
friend mat operator * (mat a, mat b)
{
mat c;
for(int i = 0; i < 3; i++){
for(int j = 0; j < 3; j++){
for(int k = 0; k < 3; k++){
c.m[i][j] += a.m[i][k] * b.m[k][j];
c.m[i][j] %= mod;
}
}
}
return c;
}
};
mat pow_mat(mat a, int b)
{
mat c;
c.init();
while(b){
if(b & 1){
c = c * a;
}
a = a * a;
b >>= 1;
}
return c;
}
int main()
{
scanf("%lld", &t);
while(t--){
scanf("%lld%lld%lld%lld%lld%lld", &a, &b, &c, &d, &p, &n);
if(n == 1){
printf("%lld\n", a);
continue;
}
mat f;
f.m[0][0] = d;
f.m[1][0] = c;
f.m[2][0] = f.m[0][1] = f.m[2][2] = 1;
mat g;
g.m[0][0] = b;
g.m[0][1] = a;
if(p >= n){
for(long long i = 3, j; i <= n; i = j + 1){
j = p / (p / i);//个数
g.m[0][2] = p / i;
mat po = pow_mat(f, min(j - i + 1, n - i + 1));
g = g * po;
}
}
else{
for(long long i = 3, j; i <= p; i = j + 1){
j = p / (p / i);
g.m[0][2] = p / i;
mat po = pow_mat(f, j - i + 1);
g = g * po;
}
mat po;
g.m[0][2] = 0;
if(p < 3){
po = pow_mat(f, n - 2);
}
else{
po = pow_mat(f, n - p);
}
g = g * po;
}
printf("%lld\n", g.m[0][0]);
}
return 0;
}
hdu 6395Sequence【矩阵快速幂】【分块】的更多相关文章
- HDU 2855 (矩阵快速幂)
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=2855 题目大意:求$S(n)=\sum_{k=0}^{n}C_{n}^{k}Fibonacci(k)$ ...
- HDU 4471 矩阵快速幂 Homework
题目链接: http://acm.hdu.edu.cn/showproblem.php?pid=4471 解题思路,矩阵快速幂····特殊点特殊处理····· 令h为计算某个数最多须知前h个数,于是写 ...
- hdu6395 (矩阵快速幂+分块)
Online Judge Online Exercise Online Teaching Online Contests Exercise Author F.A.Q Hand In Hand Onli ...
- HDU - 1575——矩阵快速幂问题
HDU - 1575 题目: A为一个方阵,则Tr A表示A的迹(就是主对角线上各项的和),现要求Tr(A^k)%9973. Input数据的第一行是一个T,表示有T组数据. 每组数据的第一行有n( ...
- hdu 1757 (矩阵快速幂) 一个简单的问题 一个简单的开始
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=1757 题意不难理解,当x小于10的时候,数列f(x)=x,当x大于等于10的时候f(x) = a0 * ...
- 随手练——HDU 5015 矩阵快速幂
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=5015 看到这个限时,我就知道这题不简单~~矩阵快速幂,找递推关系 我们假设第一列为: 23 a1 a2 ...
- HDU 3802 矩阵快速幂 化简递推式子 加一点点二次剩余知识
求$G(a,b,n,p) = (a^{\frac {p-1}{2}}+1)(b^{\frac{p-1}{2}}+1)[(\sqrt{a} + \sqrt{b})^{2F_n} + (\sqrt{a} ...
- How many ways?? HDU - 2157 矩阵快速幂
题目描述 春天到了, HDU校园里开满了花, 姹紫嫣红, 非常美丽. 葱头是个爱花的人, 看着校花校草竞相开放, 漫步校园, 心情也变得舒畅. 为了多看看这迷人的校园, 葱头决定, 每次上课都走不同的 ...
- HDU 5950 矩阵快速幂
Recursive sequence Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Other ...
- hdu 1757 矩阵快速幂 **
一看正确率这么高,以为是水题可以爽一发,结果是没怎么用过的矩阵快速幂,233 题解链接:点我 #include<iostream> #include<cstring> ; us ...
随机推荐
- go语言圣经
https://books.studygolang.com/gopl-zh/index.html
- linux环境下pytesseract的安装和央行征信中心的登录验证码识别
首先是安装,我参考的是这个 http://blog.csdn.net/xinghun_4/article/details/47860645 我是centos,使用yum yum install pyt ...
- Laravel查询构造器简介
数据表 CREATE TABLE IF NOT EXISTS students( `id` INT AUTO_INCREMENT PRIMARY KEY, `name` VARCHAR(255) NO ...
- 兼容 iOS Retina(视网膜显示) 的程序
首先我们需要明确一点,iOS设备上图片兼容retina的问题最初是由于iPhone4的分辨率由iPhone3的320X480提升到了640X960所产生. 为了让iPhone4能够兼容iPhone3上 ...
- getActionBar().setDisplayHomeAsUpEnabled(true)报空指针(已解决)
今天捣鼓了一下午.getActionBar().setDisplayHomeAsUpEnabled(true)总是报空指针.在我的还有一个Android4.4.2的项目中就没有一点问题.我还以为是我自 ...
- java中类相关注意事项
下面default类就是默认修饰符的类 1.Java中调用类中属性或方法(不管是否静态属性或方法)都要在类的方法中调用,虽然这个太基础,但今天想在类中调用静态类的静态变量,不能调用: 2.Java调用 ...
- 【转载】浅谈TDD、BDD与ATDD软件开发
转载自(此处仅供学习):http://blog.csdn.net/zhenyu5211314/article/details/22033295 1. 首先了解一下这三个开发模式都是什么意思: TDD: ...
- linux 信息收集脚本。转自insight-labs
找出所有.sh .pl .py .conf .cnf .ini .*history .*pass* (/usr/share目录里面的除外) 并且在当前目录zip打包.有些时候很多配置文件的权限配置不严 ...
- osg剔除背面开启
//设置背部剔除看不见背面东西 osg::ref_ptr<osg::CullFace> cullface=new osg::CullFace(osg::CullFace::BACK); s ...
- Kafka Java API操作topic
Kafka官方提供了两个脚本来管理topic,包括topic的增删改查.其中kafka-topics.sh负责topic的创建与删除:kafka-configs.sh脚本负责topic的修改和查询,但 ...