[Apio2010]patrol 巡逻

1912: [Apio2010]patrol 巡逻

Time Limit: 4 Sec  Memory Limit: 64 MB
Submit: 2541  Solved: 1288
[Submit][Status][Discuss]

Description

Input

第一行包含两个整数 n, K(1 ≤ K ≤ 2)。接下来 n – 1行，每行两个整数 a, b，
表示村庄a与b之间有一条道路(1 ≤ a, b ≤ n)。

Output

输出一个整数，表示新建了K 条道路后能达到的最小巡逻距离。

Sample Input

8 1

1 2

3 1

3 4

5 3

7 5

8 5

5 6

Sample Output

11

HINT

10%的数据中，n ≤ 1000, K = 1；

30%的数据中，K = 1；

80%的数据中，每个村庄相邻的村庄数不超过 25；

90%的数据中，每个村庄相邻的村庄数不超过 150；

100%的数据中，3 ≤ n ≤ 100,000, 1 ≤ K ≤ 2。

Source

[Submit][Status][Discuss]

HOME
Back

---

题解

参照AntiQuality的题解。

k=0

不过首先挖掘性质：显然的是，若只是树形图，路径最短为2n−2；并且实际上起点任意对于答案来说都是一样的

k=1

然后我们来想一想k=1的情况。比如现在我们有一颗树长成这样：



然后我们现在添加一条边：



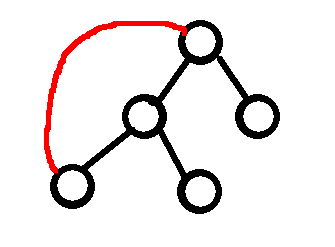
可以发现形成的环上，若环长度为lens，那么需要经过的路径就从2∗lens变为了lens+1。并且对于其他节点来说，它们的花费是不改变的。

由此自然想到我们将最长链的首尾相连，就可以得到k=1时的答案。

k=2

有了k=1，扩展至k=2的思路大致相同。除了最长链形成的环，我们需要在树上另找一条次长链。

这里有一个技巧就是把最长链上的边权全都改为-1

如果我们什么处理都没有，直接求一个次长链（次短路方法）， 可能会和最长链重合，那么最长链上的一部分就会走两遍

所以我们在求出最长链之后，把最长链上的边权赋为-1， 这样再跑一个裸的直径就好了 （这样就可以保证可以在新求出的直径中尽量少重合原先的直径）

时间复杂度\(O(n)\)

#include<bits/stdc++.h>
#define rg register
#define il inline
#define co const
template<class T>il T read(){
    rg T data=0,w=1;rg char ch=getchar();
    for(;!isdigit(ch);ch=getchar())if(ch=='-') w=-w;
    for(;isdigit(ch);ch=getchar()) data=data*10+ch-'0';
    return data*w;
}
template<class T>il T read(rg T&x) {return x=read<T>();}
typedef long long ll;
using namespace std;

co int N=1e5+6;
int n,k,d[N],fa[N];
int Head[N],Edge[N*2],Leng[N*2],Next[N*2],tot=1;
bool v[N];
void add(int x,int y,int z){
	Edge[++tot]=y,Leng[tot]=z,Next[tot]=Head[x],Head[x]=tot;
}
void dfs(int x,int&t){
	v[x]=1;
	for(int i=Head[x],y;i;i=Next[i]){
		if(v[y=Edge[i]]) continue;
		if((d[y]=d[x]+Leng[i])>=d[t]) t=y;
		fa[y]=i;
		dfs(y,t);
	}
	v[x]=0;
}
void dp(int x,int&t){
	v[x]=1;
	for(int i=Head[x],y;i;i=Next[i]){
		if(v[y=Edge[i]]) continue;
		dp(y,t);
		t=max(t,d[x]+d[y]+Leng[i]);
		d[x]=max(d[x],d[y]+Leng[i]);
	}
	v[x]=0;
}
int main(){
	read(n),read(k);
	for(int i=1,x,y;i<n;++i){
		read(x),read(y);
		add(x,y,1),add(y,x,1);
	}
	int t=1;
	dfs(1,t);
	d[t]=fa[t]=0;
	int tt=t;
	dfs(t,tt);
	int ans=2*(n-1)-(d[tt]-1);
	if(k==2){
		while(fa[tt]){
			Leng[fa[tt]]=Leng[fa[tt]^1]=-1;
			tt=Edge[fa[tt]^1];
		}
		tt=0;
		memset(d,0,sizeof d);
		dp(t,tt);
		ans-=tt-1;
	}
	printf("%d\n",ans);
	return 0;
}