Codeforces Round #556 (Div. 2) D. Three Religions 题解 动态规划

题目链接：http://codeforces.com/contest/1150/problem/D

题目大意：

你有一个参考串 s 和三个装载字符串的容器 vec[0..2] ，然后还有 q 次操作，每次操作你可以选择3个容器中的任意一个容器，往这个容器的末尾添加一个字符，或者从这个容器的末尾取出一个字符。

每一次操作之后，你都需要判断：三个容器的字符串能够表示成 s 的三个不重叠的子序列。

比如，如果你的参考串 s 是：

abdabc

而三个容器对应的字符串是：

• vec[0]：ad
• vec[1]：bc
• vec[2]：ab

那么是三个容器是可以凭借成 s 的三个不重叠的子序列的，如图：

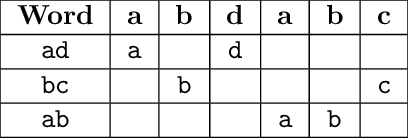
题目分析：

首先如果不是q次询问的话，那么这道题目乍看起来应该是可以使用dp或者网络流来进行求解的。

那么这道题目用dp比较好解。

首先我们需要开一个 nxt[N][26] 的数组，nxt[i][j] 表示以字符串 s[i] 开始第一个出现字符 'a'+j 的位置。N 表示字符串 s 的长度。

那么我们可以用 O(N*26) 的时间初始化这个数组。

然后我们开一个三维数组 dp[250][250][250] ，其中 dp[n0][n1][n2] 表示 字符串 s 匹配到 vec[0][n0]、vec[1][n1]、vec[2][n2] 的最小坐标。

那么我们就能够无推断出状态转移方程：

if (!i && !j && !k) dp[0][0][0] = -1;
else {
    if (i && dp[i-1][j][k]+1 < N && nxt[dp[i-1][j][k]+1][vec[0][i-1]-'a'] != INF) {
        dp[i][j][k] = min(dp[i][j][k], nxt[dp[i-1][j][k]+1][vec[0][i-1]-'a']);
    }
    if (j && dp[i][j-1][k]+1 < N && nxt[dp[i][j-1][k]+1][vec[1][j-1]-'a'] != INF) {
        dp[i][j][k] = min(dp[i][j][k], nxt[dp[i][j-1][k]+1][vec[1][j-1]-'a']);
    }
    if (k && dp[i][j][k-1]+1 < N && nxt[dp[i][j][k-1]+1][vec[2][k-1]-'a'] != INF) {
        dp[i][j][k] = min(dp[i][j][k], nxt[dp[i][j][k-1]+1][vec[2][k-1]-'a']);
    }
}

我们可以用 O(250^3) 的时间复杂度求得一个答案，然后对于q次询问，时间复杂度是 O(250^3*q)，

但是我们注意到每次更新都知识更新三个容器中任意一个的一个值。

对于减字符串操作，我们不需要进行任何处理；

而对于增加字符串操作，我们假设三个容器的字符串个数分别为 N0、N1和N2，那么：

• 当我们往 vec[0] 中添加了一个元素之后，我们除了 N0++ 操作以外，只需要更新 dp[N0][0][0]到dp[N0][N1][N2]；
• 当我们往 vec[1] 中添加了一个元素之后，我们除了 N1++ 操作以外，只需要更新 dp[0][N1][0]到dp[N0][N1][N2]；
• 当我们往 vec[2] 中添加了一个元素之后，我们除了 N2++ 操作以外，只需要更新 dp[0][0][N2]到dp[N0][N1][N2]。

所以其实对于每一次询问，我们都只需要进行 O(250^2) 就可以了。

那么最终我们将这道题目的时间复杂度降到了 O(q*250^2) 。

代码：

#include <iostream>
#include <algorithm>
#include <vector>
#include <cstdio>
using namespace std;
#define INF (1<<29)

int dp[255][255][255], n[3], nxt[100005][26], N, q;
vector<char> vec[3];
string s;

void init() {
    for (int i = 0; i < 26; i ++) {
        int idx = INF;
        for (int j = N-1; j >= 0; j --) {
            char c = (char)('a' + i);
            if (s[j] == c)
                idx = j;
            nxt[j][i] = idx;
        }
    }
}

void cal(int n0, int n1, int n2) {
    for (int i = n0; i <= n[0]; i ++) {
        for (int j = n1; j <= n[1]; j ++) {
            for (int k = n2; k <= n[2]; k ++) {
                dp[i][j][k] = INF;
                if (!i && !j && !k) dp[0][0][0] = -1;
                else {
                    if (i && dp[i-1][j][k]+1 < N && nxt[dp[i-1][j][k]+1][vec[0][i-1]-'a'] != INF) {
                        dp[i][j][k] = min(dp[i][j][k], nxt[dp[i-1][j][k]+1][vec[0][i-1]-'a']);
                    }
                    if (j && dp[i][j-1][k]+1 < N && nxt[dp[i][j-1][k]+1][vec[1][j-1]-'a'] != INF) {
                        dp[i][j][k] = min(dp[i][j][k], nxt[dp[i][j-1][k]+1][vec[1][j-1]-'a']);
                    }
                    if (k && dp[i][j][k-1]+1 < N && nxt[dp[i][j][k-1]+1][vec[2][k-1]-'a'] != INF) {
                        dp[i][j][k] = min(dp[i][j][k], nxt[dp[i][j][k-1]+1][vec[2][k-1]-'a']);
                    }
                }
            }
        }
    }
}

int main() {
    cin >> N >> q >> s;
    init();
    cal(0, 0, 0);
    while (q --) {
        string tmps1, tmps2;
        int tmpnum;
        cin >> tmps1 >> tmpnum;
        if (tmps1 == "+") {
            cin >> tmps2;
            vec[tmpnum-1].push_back(tmps2[0]);
            n[tmpnum-1] ++;
            switch(tmpnum) {
                case 1:
                    cal(n[0], 0, 0);
                    break;
                case 2:
                    cal(0, n[1], 0);
                    break;
                case 3:
                    cal(0, 0, n[2]);
                    break;
            }
        } else {
            n[tmpnum-1] --;
            vec[tmpnum-1].pop_back();
        }
        cout << ( dp[n[0]][n[1]][n[2]] == INF ? "NO" : "YES" ) << endl;
    }
    return 0;
}