LDA详解














PART 1
这个性质被叫做共轭性。共轭先验使得后验概率分布的函数形式与先验概率相同,因此使得贝叶斯分析得到了极⼤的简化。
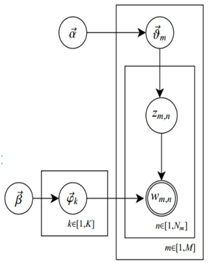
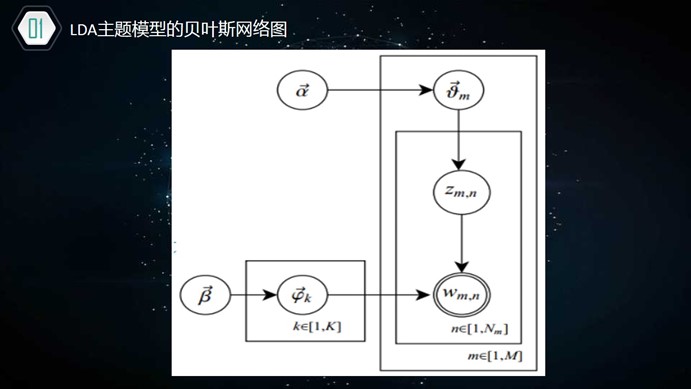
V:文档集中不重复的词汇的数目
语料库共有m篇文档,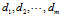 ;
;
对于文档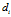 ,由
,由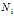 个词汇组成,可重复;
个词汇组成,可重复;
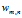 是第m个文档中的第n个词。
是第m个文档中的第n个词。
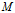 :文档集中文档的总数
:文档集中文档的总数
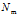 :第m个文档中包含的词汇总数
:第m个文档中包含的词汇总数
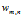 :文档m中第n个词在词典中的序号,属于1到V
:文档m中第n个词在词典中的序号,属于1到V
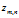 :文档m第n个词汇的主题标号,属于1到k
:文档m第n个词汇的主题标号,属于1到k
 :第k个主题的词汇分布中的参数向量
:第k个主题的词汇分布中的参数向量
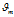 :第m文档的主题分布中的参数向量
:第m文档的主题分布中的参数向量
(1) 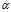 是每个文档下主题的多项式分布的Dirichlet先验参数,
是每个文档下主题的多项式分布的Dirichlet先验参数,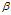 是每个主题下词的多项式分布的Dirichlet先验参数。
是每个主题下词的多项式分布的Dirichlet先验参数。
 一般事先给定,如果取0,1对称的Dirichlet分布,表示在参数学习接收后,期望每篇文档的主题不会十分集中。
一般事先给定,如果取0,1对称的Dirichlet分布,表示在参数学习接收后,期望每篇文档的主题不会十分集中。
(2) 表示第m个文档下的主题分布的分布;
表示第m个文档下的主题分布的分布;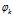 表示第k个主题下的词分布。
表示第k个主题下的词分布。
对于第i篇文档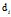 的主题分布是
的主题分布是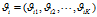 ,是长度为K的向量;
,是长度为K的向量;
对于第i篇文档的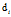 ,在主题分布
,在主题分布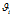 下,可以确定一个具体的主题
下,可以确定一个具体的主题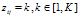 对于第K个主题
对于第K个主题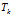 的词分布
的词分布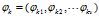 ,是长度为v的向量;
,是长度为v的向量;
由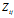 选择
选择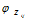 ,表示由词分布
,表示由词分布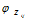 确定词,即得到观测值
确定词,即得到观测值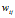 。
。
(3)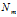 是第m个文档的单词总数。
是第m个文档的单词总数。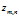 是第m个文档中第n个词的主题
是第m个文档中第n个词的主题
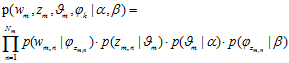
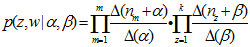
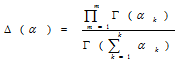
注解:
1)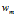 表示是第 m 篇文档的词汇序列
表示是第 m 篇文档的词汇序列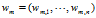
2)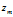 是第 m 篇文档中词汇序列对应的主题序列
是第 m 篇文档中词汇序列对应的主题序列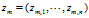
3)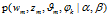 是生成此文档的生成概率
是生成此文档的生成概率
4) 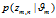 由第 m 篇文章的文档-主题分布
由第 m 篇文章的文档-主题分布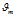 产生第 n 个词汇对应主题的概率;
产生第 n 个词汇对应主题的概率;
5)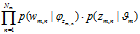 表示由
表示由 产生第 m 篇文档所有词汇的概率
产生第 m 篇文档所有词汇的概率
PART 2
Gibbs迭代规则的思想:即不考虑当前词汇的主题分配,据此词汇所在文档的主题分布以及各个主题下词汇分布来计算此词汇被分配到各个主题的概率分布,然后选择以最大概率被分配的主题。
Gibbs迭代规则公式:
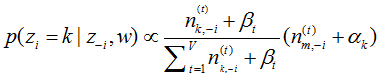
(1)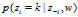 表示排除当前第i个词汇,根据文档集中其他词汇序列的主题分布来计算第i个词汇属于第k个主题的概率
表示排除当前第i个词汇,根据文档集中其他词汇序列的主题分布来计算第i个词汇属于第k个主题的概率
3)t 是第i个词汇对应词汇的字典序列号, 表示排除当前词汇,k个主题中词汇 t 出现次数。
表示排除当前词汇,k个主题中词汇 t 出现次数。
4)m 是当前词汇出现在第 m 篇文档中,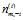 表示排除当前词汇,m 篇文档中出现词汇k的次数。
表示排除当前词汇,m 篇文档中出现词汇k的次数。
当 Gibbs 采样收敛后,跟据每个文档中主题分配次数以及每个主题中词汇分配次数来计算"文档-主题"分布和和"主题-词汇"分布。
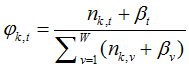
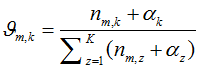
1)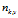 表示标号为v的词语分配到主题 k 的次数,
表示标号为v的词语分配到主题 k 的次数,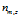 表示文档m 中所有词语分配到主题 z 的个数。
表示文档m 中所有词语分配到主题 z 的个数。
2)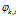 是主题在词汇上分布,式(2-10)中分子的意义是字典中第 t 个词汇分配到主题k下的次数,分母是表示的意义字典中所有词汇被分配到主题k下的次数,
是主题在词汇上分布,式(2-10)中分子的意义是字典中第 t 个词汇分配到主题k下的次数,分母是表示的意义字典中所有词汇被分配到主题k下的次数,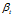 是主题-词汇分布中的先验参数,表示人为认为词汇 t 被分配到主题 k 的次数。所有词汇初始时都是等可能的被分配,以这里都假定
是主题-词汇分布中的先验参数,表示人为认为词汇 t 被分配到主题 k 的次数。所有词汇初始时都是等可能的被分配,以这里都假定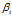 =1。
=1。
3)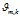 是文档-主题分布,式(2-11)中分子的意义是主题 k 被分配到第 m 篇文档中的次数,分母是表示的意义各个主题被分配到第 m 篇文档中的次数总和,文档m 的长度。
是文档-主题分布,式(2-11)中分子的意义是主题 k 被分配到第 m 篇文档中的次数,分母是表示的意义各个主题被分配到第 m 篇文档中的次数总和,文档m 的长度。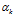 是文档-主题分布中的先验参数,表示主题 k 被分配的次数。所有主题初始时都是等可能的被分配,以这里都假定
是文档-主题分布中的先验参数,表示主题 k 被分配的次数。所有主题初始时都是等可能的被分配,以这里都假定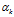 =1
=1
PART 3
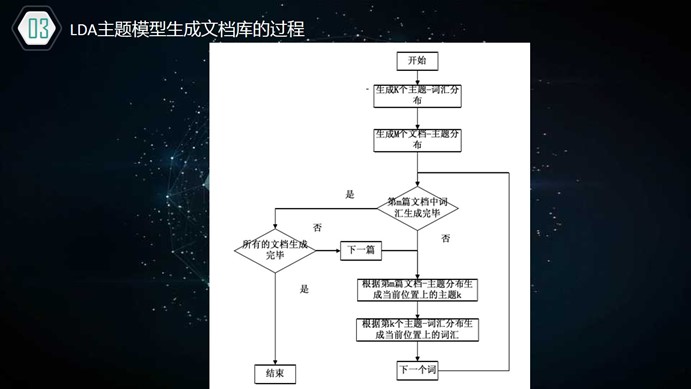
LDA主题模型生成文档语料库的过程如下:(建设生成的语料库包含m篇文档、K个主题)
(1)对于m篇文档,生成"文档-主题"分布。文档主题分布也是一个多项式分布,它的参数服从参数为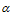 的Dirichlet先验分布。
的Dirichlet先验分布。
(2)获取每个主题下的"主题-词汇"的分布。主题-词汇分布是一个多项式分布,且它的参数变量服从参数为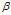 的Dirichlet先验分布。
的Dirichlet先验分布。
(3)根据 "文档-主题"、"主题-词汇"分布,依次生成所有文档中的词汇。具体做法,首先根据该文档的"文档-主题"分布规律采样一个主题,然后从这个主题对应的"主题-词汇"分布规律中采样生成一个词汇,不断重复步骤3的生成过程,直到m篇文档词汇全部生成。
LDA详解的更多相关文章
- 线性判别分析LDA详解
1 Linear Discriminant Analysis 相较于FLD(Fisher Linear Decriminant),LDA假设:1.样本数据服从正态分布,2.各类得协方差相等.虽然 ...
- PCA(主成分分析)和LDA详解
http://www.cnblogs.com/LeftNotEasy/archive/2011/01/08/lda-and-pca-machine-learning.html http://www.c ...
- LDA与最小二乘法的关系及其变种详解
1 LDA与最小二乘法的关联 对于二值分类问题,令人惊奇的是最小二乘法和LDA分析是一致的.回顾之前的线性回归,给定N个d维特征的训练样例(i从1到N),每个对应一个类标签.我们之前令y=0表示一类, ...
- Android系统目录结构详解
Android系统基于linux内核.JAVA应用,算是一个小巧精致的系统.虽是开源,但不像Linux一般庞大,娇小可亲,于是国内厂商纷纷开发出自己基于Android的操作系统.在此呼吁各大厂商眼光放 ...
- 16S 基础知识、分析工具和分析流程详解
工作中有个真理:如果你连自己所做的工作的来龙去脉都讲不清楚,那你是绝对不可能把这份工作做好的. 这适用于任何行业.如果你支支吾吾,讲不清楚,那么说难听点,你在混日子,没有静下心来工作. 检验标准:随时 ...
- 人脸验证算法Joint Bayesian详解及实现(Python版)
人脸验证算法Joint Bayesian详解及实现(Python版) Tags: JointBayesian DeepLearning Python 本博客仅为作者记录笔记之用,不免有很多细节不对之处 ...
- Linq之旅:Linq入门详解(Linq to Objects)
示例代码下载:Linq之旅:Linq入门详解(Linq to Objects) 本博文详细介绍 .NET 3.5 中引入的重要功能:Language Integrated Query(LINQ,语言集 ...
- 架构设计:远程调用服务架构设计及zookeeper技术详解(下篇)
一.下篇开头的废话 终于开写下篇了,这也是我写远程调用框架的第三篇文章,前两篇都被博客园作为[编辑推荐]的文章,很兴奋哦,嘿嘿~~~~,本人是个很臭美的人,一定得要截图为证: 今天是2014年的第一天 ...
- EntityFramework Core 1.1 Add、Attach、Update、Remove方法如何高效使用详解
前言 我比较喜欢安静,大概和我喜欢研究和琢磨技术原因相关吧,刚好到了元旦节,这几天可以好好学习下EF Core,同时在项目当中用到EF Core,借此机会给予比较深入的理解,这里我们只讲解和EF 6. ...
随机推荐
- web应用中Filter过滤器之开发应用
1 过滤器的简单开发应用部署 首先讲解过滤器的开发部署运行基本流程,在这里先通过一个简单的示例: 1)编写过滤器类 编写一个简单的过滤器类:SimpleFilter,实现Filter接口,完整的代码为 ...
- A-B Problem nyoj
A-B Problem 时间限制:1000 ms | 内存限制:65535 KB 难度:3 描述 A+B问题早已经被大家所熟知了,是不是很无聊呢?现在大家来做一下A-B吧. 现在有两个实数A和 ...
- java web 程序---javaBean
1.JavaBean 是Java中的一个组件技术,类似于微软的COM组件 SUN公司将JavaBean定义为:可以重复利用的软件组件 2.JavaBean的种类:a.可视化JavaBean b.非 ...
- 面试总结之数据结构(Data Structure)
常用数据结构及复杂度 http://www.cnblogs.com/gaochundong/p/3813252.html 常用数据结构的时间复杂度 Data Structure Add Find De ...
- 利用spring的ApplicationListener监听某一类事件的发生
1.ApplicationListener在使用过程中可以监听某一事件的发生,可以做出相应的处理,这个方式不常用,但是在特殊情况下面还是有用的. 2.导包pom.xml <project xml ...
- ueditor上传图片时目录创建失败的问题解决方法,不用那么麻烦,其实修改php/config.json这个配置文件里面的路径就行!!
ueditor的真实上传路径提示出来,我进行了如下步骤: 找到了编辑器的上传处理类 Uploader.class.php,大约110行的位置找到了上传失败的提示位置, 将 $this->stat ...
- 文件os.path相关方法
#!/usr/bin/python3# -*- coding: utf-8 -*-# @Time : 2018/6/13 15:03# @File : abspath_1.py impor ...
- React爬坑秘籍(一)——提升渲染性能
React爬坑秘籍(一)--提升渲染性能 ##前言 来到腾讯实习后,有幸八月份开始了腾讯办公助手PC端的开发.因为办公助手主推的是移动端,所以导师也是大胆的让我们实习生来技术选型并开发,他来做code ...
- Linux CentOS修改网卡IP/网关设置
1. 修改对应网卡IP的配置文件 修改以下内容 2. 修改对应网卡的网关的配置文件 vi /etc/sysconfig/network 修改以下内容 3. CentOS 修改DNS 修改以下内容 4. ...
- ConcurrentHashMap的简单理解
一.效率低下的HashTable容器HashTable容器使用synchronized来保证线程安全,但在线程竞争激烈的情况下HashTable的效率非常低下.因为当一个线程访问HashTable的同 ...

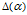 是Dirichlet
是Dirichlet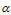 分布的
分布的