SPOJ 839 OPTM - Optimal Marks （最小割）（权值扩大，灵活应用除和取模）

http://www.spoj.com/problems/OPTM/

题意：

给出一张图，点有点权，边有边权

定义一条边的权值为其连接两点的异或和

定义一张图的权值为所有边的权值之和

已知部分点的点权，自定义其余点的点权

使图的权值最小，并在此基础上使点权和最小

输出点的权值

异或——按位做

那么题目就变成了已知一些点的点权为0/1，自定义剩余点的点权0/1

使01相遇的边最少

（01相遇指的是一条边连接的两点的点权不同）

我们建立最小割模型：

先不考虑第二问

源点向已知点的点权为0的点连正无穷的边

已知点的点权为1的点向汇点连正无穷的边

然后把原图加进去，原图中若存在u和v之间的边，就加入u向v，v向u 流量为1的边

这样最小割割的时候只会割流量为1的边，割一条边表示这条边连接的两点点权不同

最后在残量网络上，点与源点相连则代表点权为0，点与汇点相连代表点权为1

再来考虑第二问

第二问相当于最后残量网络上，点既可以与源点连又可以与汇点连的时候，选择与源点连

将所有不与源点相连的点x，加上源点向x流量为1的边

这样如果x最后选择与汇点相连，那么它就要多花费1的代价

这就使x尽可能的与源点相连

那么这岂不是影响了第一问的答案？

用点儿小技巧

原来是原图中若存在u和v之间的边，就加入u向v，v向u 流量为1的边

改成 原图中若存在u和v之间的边，就加入u向v，v向u 流量为10000的边

然后第一问相当于最最小割/10000

第二问相当于最小割%10000

最后查询与源点分离的点时，不是源点连出去的流量为1的边满流

而是dinic最后一次分层遍历遍历不到的点

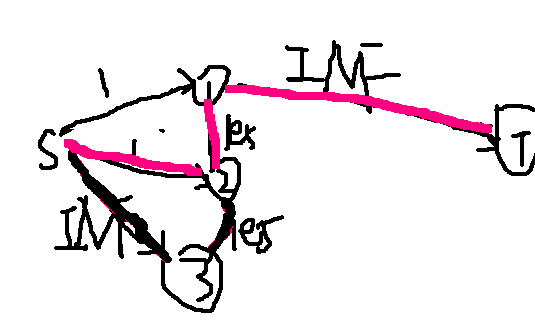
S->2的边虽然满流，但是仍可以通过S->3->2 所以2是与源点相连的点

#include<queue>
#include<cstdio>
#include<cstring>
#include<iostream>

using namespace std;

#define N 502
#define M 3001

const int inf=1e9;

struct node
{
    int u,v;
}e[];

int num[N];

int ans[N];

int front[N],to[M*],nxt[M*],cap[M*],tot;
int src,decc;
int lev[N],cur[N];

queue<int>q;

void read(int &x)
{
    x=; char c=getchar();
    while(!isdigit(c)) c=getchar();
    while(isdigit(c)) { x=x*+c-''; c=getchar(); }
}

void add(int u,int v,int w)
{
    to[++tot]=v; nxt[tot]=front[u]; front[u]=tot; cap[tot]=w;
    to[++tot]=u; nxt[tot]=front[v]; front[v]=tot; cap[tot]=;
}

bool bfs()
{
    for(int i=src;i<=decc;++i) lev[i]=-,cur[i]=front[i];
    while(!q.empty()) q.pop();
    q.push(src);
    lev[src]=;
    int now;
    while(!q.empty())
    {
        now=q.front();
        q.pop();
        for(int i=front[now];i;i=nxt[i])
            if(cap[i] && lev[to[i]]==-)
            {
                lev[to[i]]=lev[now]+;
                if(to[i]==decc) return true;
                q.push(to[i]);
            }
    }
    return false;
}

int dinic(int now,int flow)
{
    if(now==decc) return flow;
    int rest=,delta;
    for(int &i=cur[now];i;i=nxt[i])
        if(cap[i] && lev[to[i]]>lev[now])
        {
            delta=dinic(to[i],min(flow-rest,cap[i]));
            if(delta)
            {
                rest+=delta;
                cap[i]-=delta; cap[i^]+=delta;
                if(rest==flow) break;
            }
        }
    if(rest!=flow) lev[now]=-;
    return rest;
}

int main()
{
    int T,n,m,k,x;
//    int flow;
//    long long ans1,ans2;
    read(T);
    while(T--)
    {
        memset(num,-,sizeof(num));
        memset(ans,,sizeof(ans));
        //ans1=ans2=0;
        tot=;
        read(n); read(m);
        for(int i=;i<=m;++i) read(e[i].u),read(e[i].v);
        read(k);
        for(int i=;i<=k;++i)
        {
            read(x);
            read(num[x]);
        }
        decc=n+;
        for(int bit=;bit<;++bit)
        {
            memset(front,,sizeof(front));
            tot=;
            for(int i=;i<=n;++i)
                if(num[i]!=-)
                {
                    if(num[i]&<<bit) add(i,decc,inf),add(src,i,);
                    else add(src,i,inf);
                }
                else add(src,i,);
            for(int i=;i<=m;++i)
            {
                add(e[i].u,e[i].v,);
                add(e[i].v,e[i].u,);
            }
        //    flow=0;
            while(bfs())
            dinic(src,inf);
        //    ans1+=1LL*flow/10000*(1<<bit);
        //    ans2+=1LL*flow%10000*(1<<bit);
            for(int i=;i<=n;++i)
                if(lev[i]==-) ans[i]|=<<bit;
        }
    //    printf("%lld\n%lld",ans1,ans2);
        for(int i=;i<=n;++i) printf("%d\n",ans[i]);
    }
}