平面图转对偶图&19_03_21校内训练 [Everfeel]

对于每个平面图，都有唯一一个对偶图与之对应。若G‘是平面图G的对偶图，则满足：

G'中每一条边的两个节点对应着G中有公共边的面，包括最外部无限大的面。

直观地讲，红色标出来的图就是蓝色标出的图的对偶图。

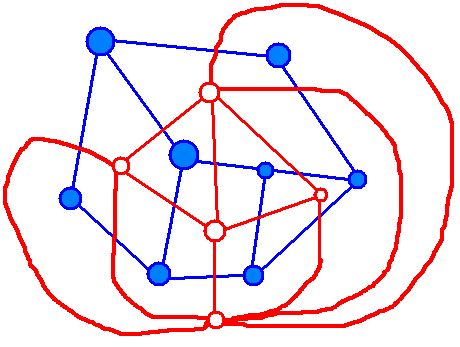
求出一个平面图的对偶图（而且不是特殊的结构），可以贪心地找出所有最小的面。但如何描述最小？我们要固定一条边，按它顺时针或逆时针的方向找到第一条边，直到出现第一个访问过的边，就找到了一个面。

具体地将：从每个边出发，按有方向的角排序，找到角度最大或最小的边，再进行下去。反正自己写写代码就知道了。

---

例题

给出一个平面图，每个点有a和b两种属性，每个面（包括无限大的面）的价值为在这个面上的点的a总和或b总和，若相邻的面所选的属性不同，代价为所有相邻点边的点权和。最大化总价值。N≤4000。

---

思路

考场上从没写过对偶图，结果自己搞出来了.......反而最小割没写出来。

转完对偶图后，从S向每个对偶图上的点连一条比边权为该面的a价值总和的边，再从这个点向T连一条边权为该面的b价值总和的边。对于原图相邻的面，连一条权值为公共边价值和的边（这个要双向）。不难发现其最小割为最小的代价。

如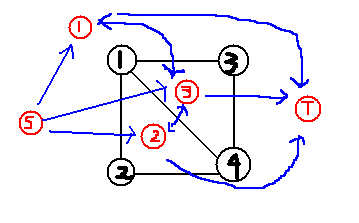：重复的边合并即可。

一个不需要代码的代码：

 #include<bits/stdc++.h>
 using namespace std;
 typedef long long int ll;
 const double pi=3.1415926535898;
 const ll maxn=2E5+;
 const ll inf=INT_MAX;
 ll min(ll x,ll y){return x<y?x:y;}
 struct pt
 {
     double x,y;
     int pos;
     pt(double a=,double b=,int p=){x=a,y=b;pos=p;}
     void operator=(pt A){x=A.x,y=A.y,pos=A.pos;}
     pt operator+(pt A){return pt(x+A.x,y+A.y,pos);}
     pt operator-(pt A){return pt(x-A.x,y-A.y,pos);}
     void out(){cout<<x<<" "<<y<<" ";}
 }p[maxn];
 ll n,m,v[maxn][],x,y,z,cur,val[maxn][],ans,dfn[maxn],ti,S,T;
 bool vis[maxn*];
 map<int,int>next;
 map<pair<int,int>,int>cost;
 set<pair<int,int> >eS;
 pt rotate(pt A,double ra){return pt(A.x*cos(ra)-A.y*sin(ra),A.x*sin(ra)+A.y*cos(ra),A.pos);}
 pt wait[maxn];
 bool cmp(pt A,pt B)
 {
     double r1=atan2(A.y,A.x);
     double r2=atan2(B.y,B.x);
     if(r1<)r1+=*pi;
     if(r2<)r2+=*pi;
     return r1<r2;
 }
 struct edge{ll to,next,from,w,bel;};
 struct graph
 {
     int head[maxn*],size;
     graph(){size=;}
     edge E[maxn*];
     void add(int u,int v,ll w)
     {
         E[++size].to=v;
         E[size].next=head[u];
         E[size].w=w;
         E[size].from=u;
         head[u]=size;
     }
     void sortAngle(pt A,pt B,int r,int num)//suppose that A is the centre
     {
         B=B-A;
         double ra=-atan2(B.y,B.x);
         B=rotate(B,ra);
         for(int i=;i<=r;++i)wait[i]=rotate(wait[i]-A,ra);
         sort(wait+,wait+r+,cmp);
         next[num]=wait[].pos;
         for(int i=;i<r;++i)
             next[wait[i].pos^]=wait[i+].pos;
         next[wait[r].pos^]=num^;
     }
     void sortAll()
     {
         for(int i=;i<=size;++i)
         {
             if(next[i]==)
             {
                 int L=;
                 for(int j=head[E[i].to];j;j=E[j].next)
                 {
                     if(E[j].to==E[i].from)continue;
                     wait[++L]=p[E[j].to];
                     wait[L].pos=j;
                 }
                 sortAngle(p[E[i].to],p[E[i].from],L,i);
             }
         }
     }
     void dfs(int i,int pos)
     {
         ans+=v[E[i].to][];
         ans+=v[E[i].to][];
         vis[i]=;
         E[i].bel=pos;
         val[pos][]+=v[E[i].to][];
         val[pos][]+=v[E[i].to][];
         i=next[i];
         if(vis[i])return;
         dfs(i,pos);
     }
     void getVal()
     {
         sortAll();
         for(int i=;i<=size;++i)
             if(!vis[i])
             {
                 ++cur;
                 dfs(i,cur);
             }
     }
     bool bfs()
     {
         for(int i=;i<=T;++i)dfn[i]=-;
         dfn[S]=;
         queue<int>Q;
         Q.push(S);
         while(Q.size())
         {
             int u=Q.front();
             Q.pop();
             for(int i=head[u];i;i=E[i].next)
             {
                 int v=E[i].to;
                 if(dfn[v]!=-||E[i].w==)continue;
                 dfn[v]=dfn[u]+;
                 Q.push(v);
             }
         }
         return dfn[T]!=-;
     }
     ll dinic(int u,ll up)
     {
         if(u==T)return up;
         ll sum=;
         for(int i=head[u];i;i=E[i].next)
         {
             int v=E[i].to;
             if(dfn[v]!=dfn[u]+||E[i].w==)continue;
             ll g=dinic(v,min(E[i].w,up-sum));
             E[i].w-=g;
             E[i^].w+=g;
             sum+=g;
             if(g==)dfn[v]=-;
             if(sum==up)break;
         }
         return sum;
     }
 }G,flow;
 int main()
 {
     freopen("everfeel.in","r",stdin);
     freopen("everfeel.out","w",stdout);
     ios::sync_with_stdio(false);
     cin>>n>>n>>m;
     for(int i=;i<=n;++i)
         cin>>p[i].x>>p[i].y>>v[i][]>>v[i][];
     for(int i=;i<=m;++i)
     {
         cin>>x>>y>>z;
         G.add(x,y,z);
         G.add(y,x,z);
     }
     G.getVal();
     S=;
     T=cur+;
     for(int i=;i<=G.size;i+=)
     {
         pair<int,int>P=make_pair(G.E[i].bel,G.E[i^].bel);
         cost[P]+=G.E[i].w;
         eS.insert(P);
     }
     for(set<pair<int,int> >::iterator pos=eS.begin();pos!=eS.end();++pos)
     {
         flow.add(pos->first,pos->second,cost[*pos]);
         flow.add(pos->second,pos->first,cost[*pos]);
     }
     for(int i=;i<=cur;++i)
     {
         flow.add(S,i,val[i][]);
         flow.add(i,S,);
         flow.add(i,T,val[i][]);
         flow.add(T,i,);
     }
     ll sum=;
     while(flow.bfs())sum+=flow.dinic(S,inf);
     cout<<ans-sum<<endl;
     return ;
 }

要数据请联系。