多源异构数据信息的融合方式0 - Dempster/Shafer 证据理论(D-S证据理论)

Dempster/Shafer 证据理论(D-S证据理论)的大体内容如下：

一、简介：

　　在理论中，由互不相容的基本命题组成的完备集合Θ称为识别框架，表示对于某一问题的所有可能答案，但是只有一个答案是正确的。D-S证据理论成为处理不确定性问题的完整理论。

　　其中，θj 称为识别框架 Θ 的一个事件或元素。接着引入幂集的概念，即识别框架 Θ 全部子集的集合，记作 2^Θ，幂集可以表示为：

　　在识别框架 Θ 中，它的任意子集 A 都对应着某问题答案的命题，可以形容这个命题为“A 是问题的答案”。其中有一个Θ(在上述公式中，最后的一个Θ)：不知道如何分配。

　　当确定了识别框架之后，接着需要建立证据信息，通常对于一个命题（该框架的子集称为命题）来说，综合分析信息之后，可以做出一个比较合适的判决，通过提出一个具体的数字，来合理的描述出对于某个命题的支持程度，这个数字也代表赋予该命题的信任度。自此建立起识别框架中命题的基本信任值的初始分配。分配给每个命题的信任程度称为基本概率分配(BPA，也称为m函数)。

　　1、在识别框架 Θ 上的基本信任分配函数 m 是一个 2Θ→[0, 1]的映射，该函数满足如下的条件：

　　m(A)为基本支持度，反映着对A的支持度的大小，其值为该命题的基本信任分配值，空集的基本信任值为零。焦元：m(A)的值大于 0。

　　2、信任函数Bel(A)表示对命题A的信任程度。公式如下所示：

　　上述公式表示了，事件A在识别框架Θ 中基本概率赋值之和，其中Bel(θ) = 1,Bel(∅) = 0。

　　3、似然函数Pl(A)表示对命题A非假的信任程度，即对A似乎可能成立的不确定性度量(对焦元A不为假的信任度的最大值)。

　　其描述的是，与事件A相交的所有BPA的和。其中，Bel与Pl的值满足Pl(A) > Bel(A)。

　　实际上，[Bel(A),Pl(A)]表示A的不确定（置信）区间，描述了对于焦元A的信任程度。[0,Bel(A)]表示命题A支持证据区间，[0,Pl(A)]表示命题A的拟信区间， [Pl(A),1]表示命题A的拒绝证据区间。Pl(A) − Bel(A)称为A的不确定度。下图为证据理论的证据区间：

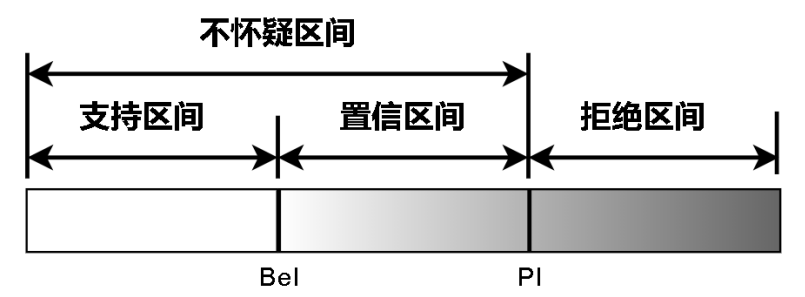
二、组合规则：

　　综合了来自多传感器的基本信度分配，得到一个新的信度分配作为输出。Dempster 组合规则的优点主要体现在证据冲突较小的情形．如果证据间存在高冲突，使用时会表现出以下缺陷：

　　　　①将100%的信任分配给小可能的命题，产生与直觉相悖的结果；

　　　　②缺乏鲁棒性，证据对命题具有一票否决权；

　　　　③对基本信度分配很敏感．在实际的数据处理中，证据冲突的情况经常遇到，所以要设法避免冲突证据组合产生的错误，否则会产生错误结论。

　　为解决此问题，有两种途径：

　　　　1、使用其它组合规则，如Yager规则，D&P规则，Murphy平均规则等等；其中Murphy 法的合成规则如下：

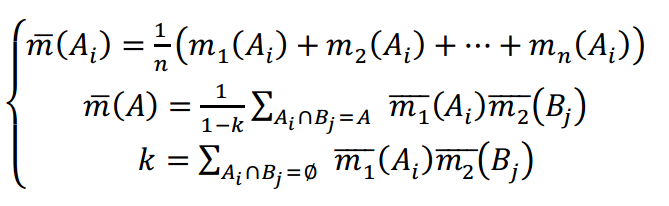
　　　　其中，Murphy的方法对证据源进行了权值平均达到对其修正的目的，减轻了证据冲突对其的影响，也解决了一票否决的问题，避免零概率赋值的影响。当然了不足之处在于，没有注意到证据之间存在的关联性。

　　　　2、对原证据进行预处理，如进行折扣。

　　D-S证据理论的最新发展和应用的方向有：

　　　　基于规则的证据推理模型及其规则库的离线和在线更新决策模型

　　　　证据理论与支持向量机的结合

　　　　证据理论与粗糙集理论的结合

　　　　证据理论与模糊集理论的结合

　　　　证据理论与神经网络的结合

　　　　基于数据的 Markovian 与 Dirichlet 混合方法实现对证据理论质函数的赋值。

三、理论+实践过程：

　　设m1和m2是由两个独立的证据源（传感器）导出的基本概率分配函数，Bel1和Bel2为识别框架 θ 上的信任度函数，则Dempster组合规则可以计算这两个证据共同作用产生的反映融合信息的新的基本概率分配函数，且焦元集合分别为A1,A2,A3,...,Ai和B1,B2,B3,...,Bj，过程图如下所示：　　

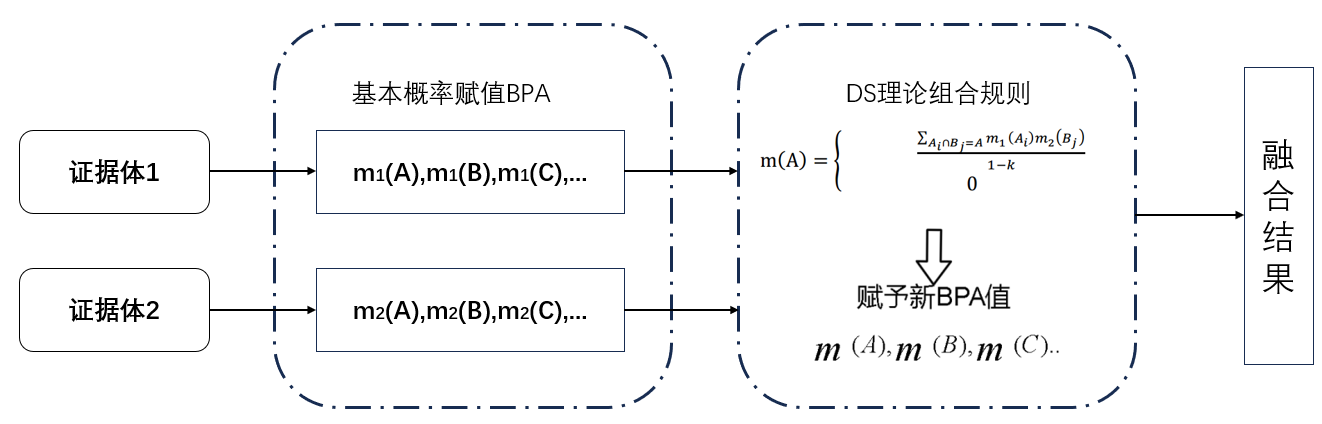
　　其中k代表矛盾因子，反映了不同证据之间的矛盾系数，其中，k值越高则冲突程度越高，通过1-k可以避免将非0概率赋给空集∅，依次来满足概率分配的基本要求。

　　多个证据之间的融合如下所示：

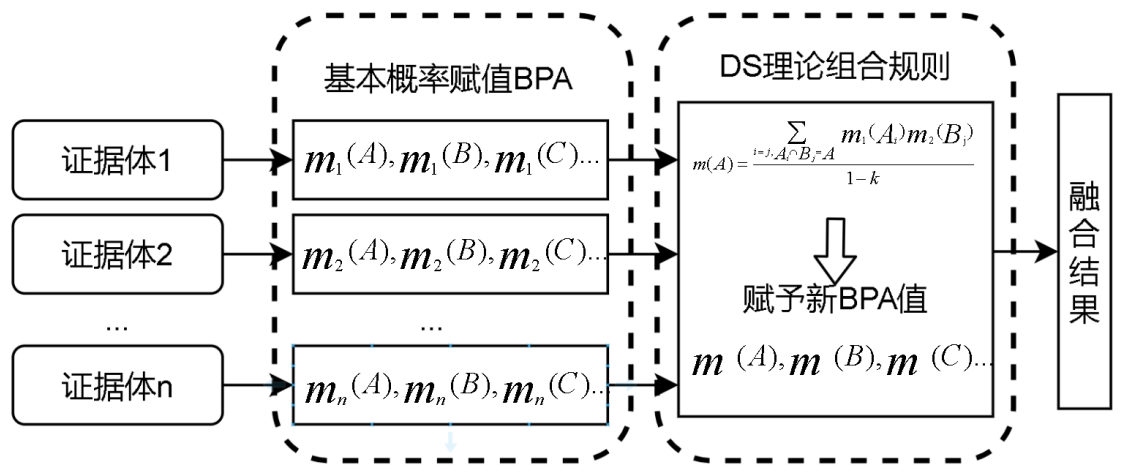
　　　　对于多个证据的合成，计算思路是一样的，无非就是使用正交和的方式进行处理，产生一个新的m函数，计算过程顺序对结果没有任何影响。

例子介绍：假如店里有好几个店员，然后来了一个新的漂亮的女店员小红，他们根据自己的判断提供了谁到底喜欢小红的证据信息，综合起来为：
　　　　

　　　　E1:m1({小A})=0.5,m1({小B})=0.2,m1({小C，小D})=0.2，m1( Θ )=0.1；
　　　　E2:m2({小A})=0.3,m2({小B})=0.3,m2({小C，小D})=0.2，m2( Θ )=0.2；
　　　　E3:m3({小A})=0.2,m3({小B})=0.2,m3({小C，小D})=0.1，m3( Θ )=0.5。

首先，我们先计算新合成的m({小A}) 值，即三条证据命题集合交集为{小A}的信任值乘积之和

　　　　1、m({小A}) =[ m1({小A})+m1( Θ )] * [m2({小A}) + m2( Θ )]*[ m3({小A}) + m3( Θ )] - [m1( Θ ) * m2(Θ) * m3(Θ)]=0.2

　　　　2、m({小B})=0.065

　　　　3、m({小C，小D})= 0.062

　　　　4、m( Θ )=0.01。

　　　　再进行归一化处理，可知1-K = m({小A}) + m({小B}) + m({小C，小D}) +m(Θ)=0.337。

　　　　因此，最终结果应该为：m({小A})=0.593,m({小B})=0.193,m({小C，小D})=0.184，m3( Θ )=0.03。

　但是数据合并的时候，明显存在着许多的问题，利用经典Dempster组合规则容易易产生悖论，存在几种典型的悖论情况：

　　1、常规冲突问题：多个证据之间存在强烈的冲突，融合后的结果明显不合理。甚至都不能采用合成规则进行合成。

　　2、一票否决问题，某一个命题中，存在基本信任分配为0。

　　3、鲁棒性不佳问题，因为 Dempster组合规则对冲突信息处理有误。

新增加的知识点：

　　D-S的主要概念是对某一种概率的扩展，但是它使用的不是一个值，而是区间，区间的下限是对可能发生的事情的信任，区间的上限是可信度。

　　D-S证据理论的功能如下：组合、获取质量、获取信念、获取可信度、过滤结果、获取最终结果。

　　假设：有一个网站/资源收集用户观看电影的评论。每个用户都可以为特定类型或一组类型投票，并具有一定的置信度（比方说，对某部电影的评论可以是这样的：西部片60%，动作片30%，战争片20%）。该算法可以帮助合并所有评论，从而得到最终结果。