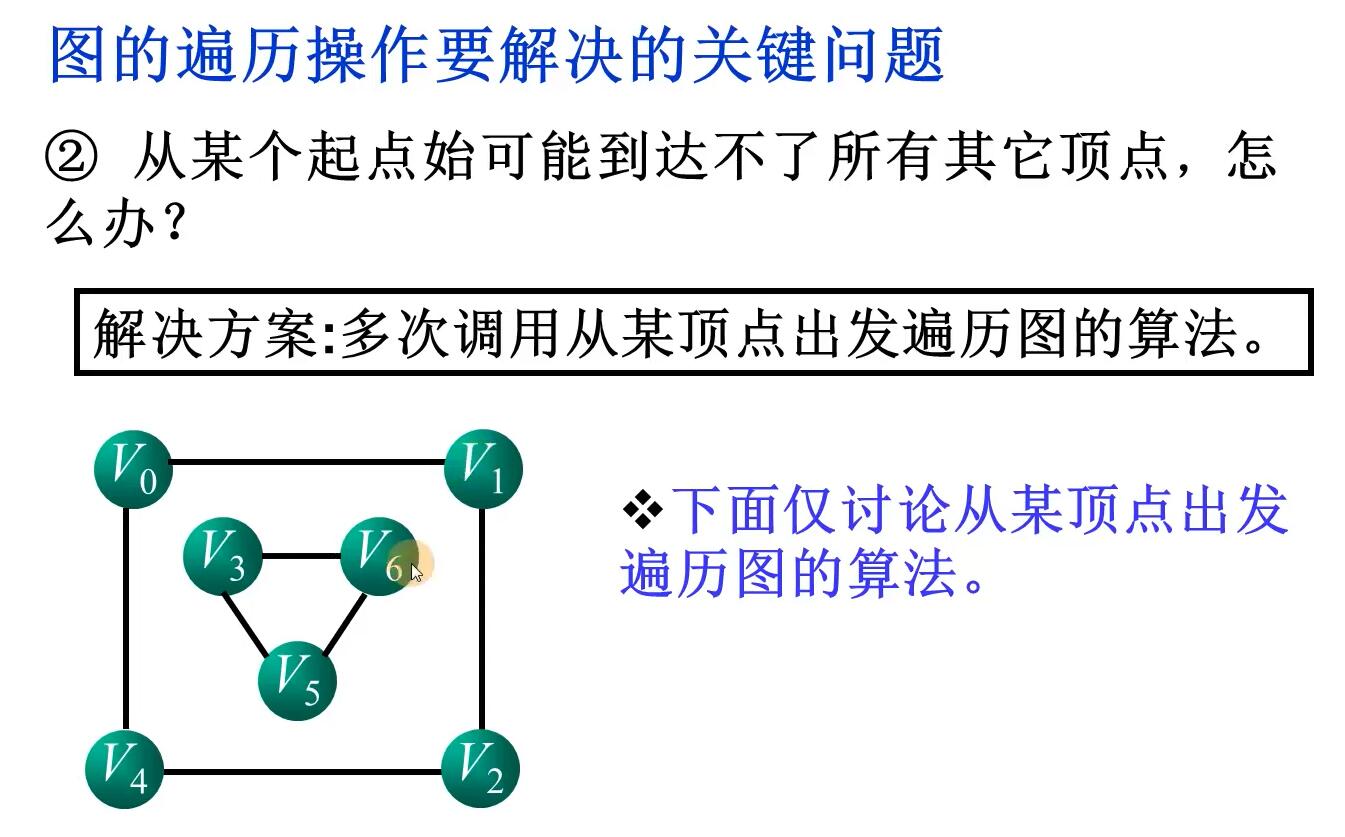
图的遍历(DFS和BFS)
声明:图片及内容基于https://www.bilibili.com/video/BV1rp4y1Q72r?from=articleDetail
图的遍历



深度优先遍历(DFS)
DFS核心是递归和栈
原理


邻接矩阵DFS代码
template <class T>
void MGraph<T>::DFS(int i){
cout<<vertex[i]<<" ";
visit[i]=1;
for(int j=0;j<vertexNum;j++){ //对邻接矩阵的第i行的每一列遍历
if(visit[j]==0&&arc[i][j]!=0&&arc[i][j]!=INFINIT){
DFS(j);
}
}
}
template <class T>
void MGraph<T>::DFSTraverse(){
for(int i=0;i<vertexNum;i++){ //visit数组初始化
visit[i]=0;
}
for(int i=0;i<vertexNum;i++){
if(!visit[i])
DFS(i);
}
}
完整代码
#include<iostream>
#define MAXVAX 100
using namespace std;
const int INFINIT=65535;
int visit[MAXVAX];
template <class T>
class MGraph {
private:
T *vertex; //顶点信息
int **arc; //邻接矩阵
int vertexNum,arcNum; //顶点数,边数
public:
MGraph(T v[],int n,int e);
~MGraph();
void DFS(int i);
void DFSTraverse();
void display();
};
template <class T>
void MGraph<T>::DFS(int i){
cout<<vertex[i]<<" ";
visit[i]=1;
for(int j=0;j<vertexNum;j++){
if(visit[j]==0&&arc[i][j]!=0&&arc[i][j]!=INFINIT){
DFS(j);
}
}
} template <class T>
void MGraph<T>::DFSTraverse(){
for(int i=0;i<vertexNum;i++){
visit[i]=0;
}
for(int i=0;i<vertexNum;i++){
if(!visit[i])
DFS(i);
}
}
template <class T>
MGraph<T>::MGraph(T v[],int n,int e) { //n是顶点数,e是边数
vertexNum=n;
arcNum=e;
vertex = new T[vertexNum]; //建立顶点信息
arc = new int*[vertexNum]; //建立邻接表
for(int i=0; i<vertexNum; i++)
arc[i]=new int[vertexNum]; for(int i=0; i<vertexNum; i++) { //初始化顶点信息
vertex[i]=v[i];
}
for(int i=0;i<vertexNum;i++) //初始化邻接表
for(int j=0;j<vertexNum;j++){
if(i==j) arc[i][j]=0;
else arc[i][j]=INFINIT;
} int vi,vj,w;
for(int i=0;i<arcNum;i++){
cout<<"请输入边的两个顶点和这条边的权值"<<endl;
cin>>vi>>vj>>w; //输入边依附的两个顶点的编号 和权值
arc[vi][vj]=w; //有边标志
}
} template <class T>
void MGraph<T>::display(){
for(int i=0;i<vertexNum;i++){
for(int j=0;j<vertexNum;j++){
cout<<arc[i][j]<<"\t";
}
cout<<endl;
}
cout<<endl; for(int i=0;i<vertexNum;i++){
cout<<vertex[i]<<" ";
}
cout<<endl;
} template <class T>
MGraph<T>::~MGraph(){
delete []vertex;
for(int i=0;i<vertexNum;i++)
delete [] arc[i];
delete [] arc;
}
int main(){
const char* v[5]={"v0","v1","v2","v3","v4"};
MGraph<const char*> mgraph(v,5,6);
mgraph.display();
mgraph.DFSTraverse();
return 0;
}
邻接表DFS代码
void ALGraph::DFS(int v){
visited[v]=1;
cout<<adjList[v].vertex<<" ";
ArcNode *p=adjList[v].firstEdge;
while(p){
if(!visited[p->adjvex])
DFS(p->adjvex);
p=p->next;
}
}
void ALGraph::DFSTraverse(){
int i;
for(i=0;i<vertexNum;i++){
visited[i]=0;
}
for(i=0;i<vertexNum;i++){
if(!visited[i]){
DFS(i);
}
}
}
完整代码
#include<iostream>
#include<string.h>
using namespace std;
const int MAX=10;
int visited[4]={0,0,0,0};
typedef struct ArcNode{ //边结点
int adjvex;
ArcNode *next;
}ArcNode;
typedef struct { //表头
int vertex;
ArcNode *firstEdge;
}VertexNode[MAX];
class ALGraph{
private:
int vertexNum;
int arcNum;
VertexNode adjList;
public:
ALGraph(int v[],int n,int e);
void display();
void DFS(int v);
void DFSTraverse();
};
void ALGraph::DFSTraverse(){
int i;
for(i=0;i<vertexNum;i++){
visited[i]=0;
}
for(i=0;i<vertexNum;i++){
if(!visited[i]){
DFS(i);
}
}
}
void ALGraph::DFS(int v){ visited[v]=1;
cout<<adjList[v].vertex<<" ";
ArcNode *p=adjList[v].firstEdge;
while(p){
if(!visited[p->adjvex])
DFS(p->adjvex);
p=p->next;
}
}
ALGraph::ALGraph(int v[],int n,int e){
vertexNum=n;
arcNum=e;
for(int i=0;i<vertexNum;i++){
adjList[i].vertex=v[i];
adjList[i].firstEdge=NULL;
}
int vi,vj;
ArcNode *s;
for(int i=0;i<arcNum;i++){
cout<<"请输入第"<<i+1<<"条边的两个顶点在数组中的坐标"<<endl;
cin>>vi>>vj;
s=new ArcNode;
s->adjvex=vj;
s->next=adjList[vi].firstEdge;
adjList[vi].firstEdge=s;
s=new ArcNode;
s->adjvex=vi;
s->next=adjList[vj].firstEdge;
adjList[vj].firstEdge=s;
}
}
void ALGraph::display(){
for(int i=0;i<vertexNum;i++){
ArcNode *p=adjList[i].firstEdge;
cout<<adjList[i].vertex;
if(p) cout<<"->";
while(p){
cout<<p->adjvex<<" ";
p=p->next;
if(p) cout<<"->";
}
cout<<endl;
}
}
int main(){
int v[4]={0,1,2,3};
ALGraph algraph(v,4,4);
algraph.display();
algraph.DFSTraverse();
return 0;
}
广度优先遍历(BFS)
BFS核心是队列
原理


邻接矩阵BFS代码
template <class T>
void MGraph<T>::BFS(int i) {
queue<int> q;
visit[i]=1;
q.push(i);
while(!q.empty()) {
int t=q.front();
cout<<vertex[t]<<" ";
q.pop();
for(int j=0; j<vertexNum; j++) {
if(!vertex[i]&&arc[i][j]!=0&&arc[i][j]!=INFINIT) {
visit[j]=1;
q.push(j);
}
}
}
}
template <class T>
void MGraph<T>::BFSTraverse() {
for(int i=0; i<vertexNum; i++) { //visit数组初始化
visit[i]=0;
}
for(int i=0; i<vertexNum; i++) { //BFS
if(!visit[i])
BFS(i);
}
}
完整代码
#include<iostream>
#include<queue>
#define MAXVAX 100
using namespace std;
const int INFINIT=65535;
int visit[MAXVAX];
template <class T>
class MGraph {
private:
T *vertex; //顶点信息
int **arc; //邻接矩阵
int vertexNum,arcNum; //顶点数,边数
public:
MGraph(T v[],int n,int e);
~MGraph();void display();
void BFS(int i);
void BFSTraverse();
}; template <class T>
void MGraph<T>::BFS(int i) {
queue<int> q;
visit[i]=1;
q.push(i);
while(!q.empty()) {
int t=q.front();
cout<<vertex[t]<<" ";
q.pop();
for(int j=0; j<vertexNum; j++) {
if(!vertex[i]&&arc[i][j]!=0&&arc[i][j]!=INFINIT) {
visit[j]=1;
q.push(j);
}
}
}
} template <class T>
void MGraph<T>::BFSTraverse() {
for(int i=0; i<vertexNum; i++) { //visit数组初始化
visit[i]=0;
}
for(int i=0; i<vertexNum; i++) {
if(!visit[i])
BFS(i);
}
}
template <class T>
MGraph<T>::MGraph(T v[],int n,int e) { //n是顶点数,e是边数
vertexNum=n;
arcNum=e;
vertex = new T[vertexNum]; //建立顶点信息
arc = new int*[vertexNum]; //建立邻接表
for(int i=0; i<vertexNum; i++)
arc[i]=new int[vertexNum]; for(int i=0; i<vertexNum; i++) { //初始化顶点信息
vertex[i]=v[i];
}
for(int i=0; i<vertexNum; i++) //初始化邻接表
for(int j=0; j<vertexNum; j++) {
if(i==j) arc[i][j]=0;
else arc[i][j]=INFINIT;
} int vi,vj,w;
for(int i=0; i<arcNum; i++) {
cout<<"请输入边的两个顶点和这条边的权值"<<endl;
cin>>vi>>vj>>w; //输入边依附的两个顶点的编号 和权值
arc[vi][vj]=w; //有边标志
}
} template <class T>
void MGraph<T>::display() {
for(int i=0; i<vertexNum; i++) {
for(int j=0; j<vertexNum; j++) {
cout<<arc[i][j]<<"\t";
}
cout<<endl;
}
cout<<endl; for(int i=0; i<vertexNum; i++) {
cout<<vertex[i]<<" ";
}
cout<<endl;
} template <class T>
MGraph<T>::~MGraph() {
delete []vertex;
for(int i=0; i<vertexNum; i++)
delete [] arc[i];
delete [] arc;
}
int main() {
const char* v[5]= {"v0","v1","v2","v3","v4"};
MGraph<const char*> mgraph(v,5,6);
mgraph.display();
mgraph.BFSTraverse();
return 0;
}
邻接表BFS代码
void ALGraph::BFS(int i){
queue<int> q;
visited[i]=1;
q.push(i);
while(!q.empty()){
int t=q.front();
cout<<adjList[t].vertex<<" ";
q.pop();
ArcNode *p=adjList[i].firstEdge;
while(p){
if(!visited[p->adjvex]){
q.push(p->adjvex);
visited[p->adjvex]=1;
}
p=p->next;
}
}
}
void ALGraph::BFSTraverse(){
int i;
for(i=0;i<vertexNum;i++){
visited[i]=0;
}
for(i=0;i<vertexNum;i++){
if(!visited[i]){
BFS(i);
}
}
}
完整代码
#include<iostream>
#include<string.h>
#include<queue>
using namespace std;
const int MAX=10;
int visited[4]={0,0,0,0};
typedef struct ArcNode{ //边结点
int adjvex;
ArcNode *next;
}ArcNode;
typedef struct { //表头
int vertex;
ArcNode *firstEdge;
}VertexNode[MAX];
class ALGraph{
private:
int vertexNum;
int arcNum;
VertexNode adjList;
public:
ALGraph(int v[],int n,int e);
void display();void BFS(int v);
void BFSTraverse();
};
void ALGraph::BFS(int i){
queue<int> q;
visited[i]=1;
q.push(i); while(!q.empty()){
int t=q.front();
cout<<adjList[t].vertex<<" ";
q.pop();
ArcNode *p=adjList[i].firstEdge;
while(p){
if(!visited[p->adjvex]){
q.push(p->adjvex);
visited[p->adjvex]=1;
}
p=p->next;
}
}
}
void ALGraph::BFSTraverse(){
int i;
for(i=0;i<vertexNum;i++){
visited[i]=0;
}
for(i=0;i<vertexNum;i++){
if(!visited[i]){
BFS(i);
}
}
} ALGraph::ALGraph(int v[],int n,int e){
vertexNum=n;
arcNum=e;
for(int i=0;i<vertexNum;i++){
adjList[i].vertex=v[i];
adjList[i].firstEdge=NULL;
}
int vi,vj;
ArcNode *s;
for(int i=0;i<arcNum;i++){
cout<<"请输入第"<<i+1<<"条边的两个顶点在数组中的坐标"<<endl;
cin>>vi>>vj;
s=new ArcNode;
s->adjvex=vj;
s->next=adjList[vi].firstEdge;
adjList[vi].firstEdge=s;
s=new ArcNode;
s->adjvex=vi;
s->next=adjList[vj].firstEdge;
adjList[vj].firstEdge=s;
}
}
void ALGraph::display(){
for(int i=0;i<vertexNum;i++){
ArcNode *p=adjList[i].firstEdge;
cout<<adjList[i].vertex;
if(p) cout<<"->";
while(p){
cout<<p->adjvex<<" ";
p=p->next;
if(p) cout<<"->";
}
cout<<endl;
}
}
int main(){
int v[4]={0,1,2,3};
ALGraph algraph(v,4,4);
algraph.display();
algraph.BFSTraverse();
return 0;
}
图的遍历(DFS和BFS)的更多相关文章
- 图的遍历——DFS和BFS模板(一般的图)
关于图的遍历,通常有深度优先搜索(DFS)和广度优先搜索(BFS),本文结合一般的图结构(邻接矩阵和邻接表),给出两种遍历算法的模板 1.深度优先搜索(DFS) #include<iostrea ...
- 图的遍历(DFS、BFS)
理论: 深度优先搜索(Depth_Fisrst Search)遍历类似于树的先根遍历,是树的先根遍历的推广: 广度优先搜索(Breadth_First Search) 遍历类似于树的按层次遍历的过程: ...
- 图的遍历DFS
图的遍历DFS 与树的深度优先遍历之间的联系 树的深度优先遍历分为:先根,后根 //树的先根遍历 void PreOrder(TreeNode *R){ if(R!=NULL){ visit(R); ...
- 图的遍历[DFS][BFS]
#include<iostream> #include<iostream> #include<cstring> #include<queue> #inc ...
- 图的遍历——DFS
原创 图的遍历有DFS和BFS两种,现选用DFS遍历图. 存储图用邻接矩阵,图有v个顶点,e条边,邻接矩阵就是一个VxV的矩阵: 若顶点1和顶点5之间有连线,则矩阵元素[1,5]置1,若是无向图[5, ...
- 图的遍历——DFS(矩形空间)
首先,这里的图不是指的我们一般所说的图结构,而是大小为M*N的矩形区域(也可以看成是一个矩阵).而关于矩形区域的遍历问题经常出现,如“寻找矩阵中的路径”.“找到矩形区域的某个特殊点”等等之类的题目,在 ...
- 图的遍历---DFS
类型一:邻接表 题目一:员工的重要性 题目描述 给定一个保存员工信息的数据结构,它包含了员工唯一的id,重要度 和 直系下属的id. 比如,员工1是员工2的领导,员工2是员工3的领导.他们相应的重要度 ...
- 图的遍历——DFS(邻接矩阵)
递归 + 标记 一个连通图只要DFS一次,即可打印所有的点. #include <iostream> #include <cstdio> #include <cstdli ...
- 16.boost图深度优先遍历DFS
#include <iostream> #include <boost/config.hpp> //图(矩阵实现) #include <boost/graph/adjac ...
- 图的数据结构的实现与遍历(DFS,BFS)
//图的存储结构:const int MAXSIZE = 10;//邻接矩阵template<class T>class MGraph {public: MGraph(T a[], ...
随机推荐
- Windows和Linux下通过go实现自删除
自删除在攻防中都挺常见的,自写远控通常也有需要.可是在度娘里搜不到什么办法,于是就查查Windows api学习记录一回. linux 先获得当前程序的文件名,再使用syscall这个包中的Unlin ...
- OpenSSL命令总结
OpenSSL命令总结 疑今者察之古,不知来者视之往. 导航 介绍 对称加密 公钥加密 信息摘要 数字证书 杂项 介绍 密码学标准和互联网协议一样,是一种大家都遵守的约定和标准,比如PKCS#1中规定 ...
- MIGO新增页签增强
1.文档说明 本方法是将新增字段,展示在MIGO的新增页签中,并保存到自建表. 新增页签的方法,和采购订单新增页签的方法原理基本一致,都是需要创建函数组,并实现相应方法和屏幕,并在增强中调用该函数组, ...
- 2023-08-18:用go写算法。你会得到一个字符串 text, 你应该把它分成 k 个子字符串 (subtext1, subtext2,…, subtextk)。 要求满足: subtexti 是
2023-08-18:用go写算法.你会得到一个字符串 text, 你应该把它分成 k 个子字符串 (subtext1, subtext2,-, subtextk). 要求满足: subtexti 是 ...
- 数仓性能优化:倾斜优化-表达式计算倾斜的hint优化
本文分享自华为云社区<GaussDB(DWS)性能调优:倾斜优化-表达式计算倾斜的hint优化>,作者: 譡里个檔 . 1.原始SQL SELECT TMP4.TAX_AMT, CATE. ...
- 人人都在聊的云原生数据库Serverless到底是什么?
摘要:华为云数据库营销专家Tony Chen和华为云数据库高级产品经理佳恩开展了一场关于云原生数据库与Serverless结合的直播对话. 云计算的迅猛发展推动了数据库的变革,云原生数据库成为当前数据 ...
- 买家手册:企业在选择 SBOM 供应商时需要注意什么?
Apache Log4j 和 Log4Shell 两大事件的发生,将软件物料清单(Software Bill of Materials, SBOM)推向安全防护前沿,成为企业保护其软件供应链的方式之一 ...
- 火山引擎A/B测试在消费行业的案例实践
更多技术交流.求职机会,欢迎关注字节跳动数据平台微信公众号,回复[1]进入官方交流群 近日,火山引擎数智平台举办了"走进火山-全链路增长:数据飞轮转动消费新生力"的活动,其中火山引 ...
- Excel 2016 VBA 提取单元格的中文字符
启用开发工具 方式一:[右键Sheet1 ]->[查看代码] 方式二:[开发者工具]->[Visual Basic] Function chinese(rng As String) Dim ...
- Selenium八大元素定位(元素定位,元素等待)
Selenium WebDriver查找页面元素及元素操作 元素常用方法定位方法 通过id定位元素:find_element_by_id('id_value') 通过name定位元素:find_ele ...
