oeasy教您玩转vim - 23 - 配置文件

配置文件

回忆上节课内容

• 我们上次找到配置文件的位置 ~/.vimrc

  • 了解各种配置开关
  • 修改配置文件并应用
• 这次想了解和配色方案相关的内容

colorscheme

• vi ~/.vimrc.old 中发现 colorscheme 属性

• 可以选择 blue 试试
• :colorscheme blue

智能提示

• 配色方案 colorscheme 的提示是怎么来的？
• 如果没有提示的话

• :set wildmode? 看一下

  • 默认是 longest,list,full

• 如果:set wildmod=

  • 智能提示就没有了

• :set wildmode=longest,list,full

  • 又会出现

• 还可以调出菜单 :set wildmenu

  • 如果 :set nowildmenu 就没有菜单了

    • 再:colorscheme tab 就没有用了
  • tab 其实就是 wildchar
  • 用来获取提示的

选择配色方案

• 在命令行模式中输入 :colorscheme tab

  • 看到提示的配色方案
  • 用 tab 列出可选项
  • 然后选择一个配色方案
• 其实各种颜色可以来一个个的试试

配色方案举例

• 你觉得哪个好看呢？

色彩模式选择

• 都试了一遍，觉得 murphy 或 blue 还行
• :set t_Co? 查看当前色彩模式
• :set t_Co=256 色彩模式设置为 256 色
• :set t_Co& 色彩模式设置为默认
• 观察颜色的细微变化
• :h 't_Co' 查询帮助

• t 是 terminal终端
• Co 是 Color颜色

• 我们把这些写进配置文件 ~/.vimrc

  • set t_Co=256
  • colorscheme blue

颜色模式的作用

• 这对于软件界面改变很大

  • 我们可以比较清晰地看到关键字、字符串、函数名等
  • 但是对于编写的程序和文本本身的内容
  • 并没有什么影响
• 只是比较好看的蓝布棉门帘

配置文件

• set statusline=%-040.40(%F%m%)%-030.30([%l,%c]%)%p%%
• set laststatus=2
• set ruler
• set number
• set showcmd
• set nocompatible
• set showcmd
• set showmode
• set history=100
• set t_Co=256
• colorscheme blue

更多细节

• :h colorscheme 可以找到配色方案的帮助

配色文件夹

#找到vim的位置
whereis vim
#找到colors的位置
find /usr/share/vim -name "colors"

网上寻找合适的配色方案

• 网址是 https://vimcolors.com/
• 选到合适的配色之后可以进入 github 去下载相应的配色文件
• 把下载的 .vim 文件放进 colors 文件夹就可以了
• 使用 :colorscheme XXX 应用该配色方案

下载颜色方案

#下载颜色方案
git clone https://github.com/gryf/wombat256grf.git
#放到相应文件夹里
sudo cp ./wombat256grf/wombat256grf.vim /usr/share/vim/vim81/colors
#运行
vi oeasy.java

• :colorscheme wombat256grf
• 颜色设置成功

把当前配色方案输出到 html

• :TOhtml

• 可以把当前的配色方案输出为网页格式

  • :w oeasy.html

• 转化过程是一个vim文件

  • 也可以直接运行
  • :source $VIMRUNTIME/syntax/2html.vim

增加自己的配色方案

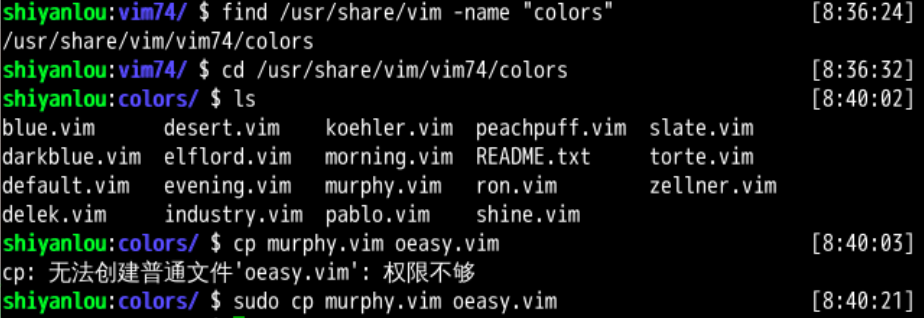
#找到colors的位置
cd /usr/share/vim/vim81/colors
#列出所有配色方案
ls
#复制出自己的配色方案
sudo cp murphy.vim oeasy.vim

总结

• 这次我们研究了配色方案

  • 找到了 colors 的位置
  • 下载并应用了颜色方案
  • 制作了自己的配色方案

• 下面我想修改配色方案的颜色

  • 最后在vim中尝试 :colorscheme oeasy
  • 是否能成功？？？
• 下次再说