TreeMap - 红黑树

TreeMap是Map家族中的一员，也是用来存放key-value键值对的。平时在工作中使用的可能并不多，它最大的特点是遍历时是有顺序的，根据key的排序规则来

TreeMap是一个双列集合，是Map的子类。底层由红黑树结构构成。

TreeMap是一个基于key有序的key value散列表。

• map根据其键的自然顺序排序，或者根据map创建时提供的Comparator排序
• 不是线程安全的
• key 不可以存入null
• 底层是基于红黑树实现的

特点：

• 元素中键不能重复
• 元素会按照大小顺序排序

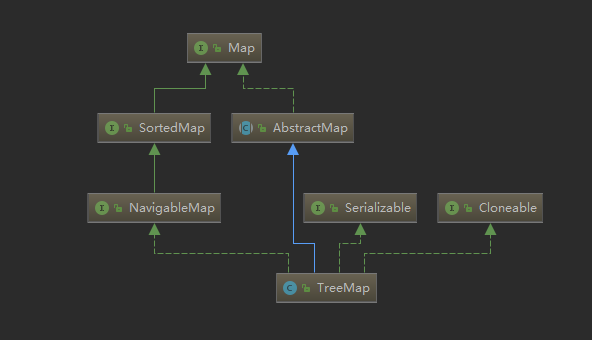
以上是TreeMap的类结构图：

• 实现了NavigableMap接口，NavigableMap又实现了Map接口，提供了导航相关的方法。
• 继承了AbstractMap，该方法实现Map操作的骨干逻辑。
• 实现了Cloneable接口，标记该类支持clone方法复制
• 实现了Serializable接口，标记该类支持序列化

package com.hankcs.book.ch02;

import java.util.Map;
import java.util.TreeMap;

public class TreeTest {
    public static void main(String[] args) {

        Map<Integer, String> treeMap = new TreeMap<>();
        treeMap.put(16, "a");
        treeMap.put(1, "b");
        treeMap.put(4, "c");
        treeMap.put(3, "d");
        treeMap.put(8, "e");
        // 遍历
        System.out.println("默认排序：");
        treeMap.forEach((key, value) -> {
            System.out.println("key: " + key + ", value: " + value);
        });

        // 构造方法传入比较器
        Map<Integer, String> tree2Map = new TreeMap<>((o1, o2) -> o2 - o1);
        tree2Map.put(16, "a");
        tree2Map.put(1, "b");
        tree2Map.put(4, "c");
        tree2Map.put(3, "d");
        tree2Map.put(8, "e");
        // 遍历
        System.out.println("倒序排序：");
        tree2Map.forEach((key, value) -> {
            System.out.println("key: " + key + ", value: " + value);
        });
    }
}

输出：

默认排序：
key: 1, value: b
key: 3, value: d
key: 4, value: c
key: 8, value: e
key: 16, value: a
倒序排序：
key: 16, value: a
key: 8, value: e
key: 4, value: c
key: 3, value: d
key: 1, value: b

实现原理

了解一下红黑树的特点：红黑树是一颗自平衡的排序二叉树。先从二叉树开始说起。

二叉树

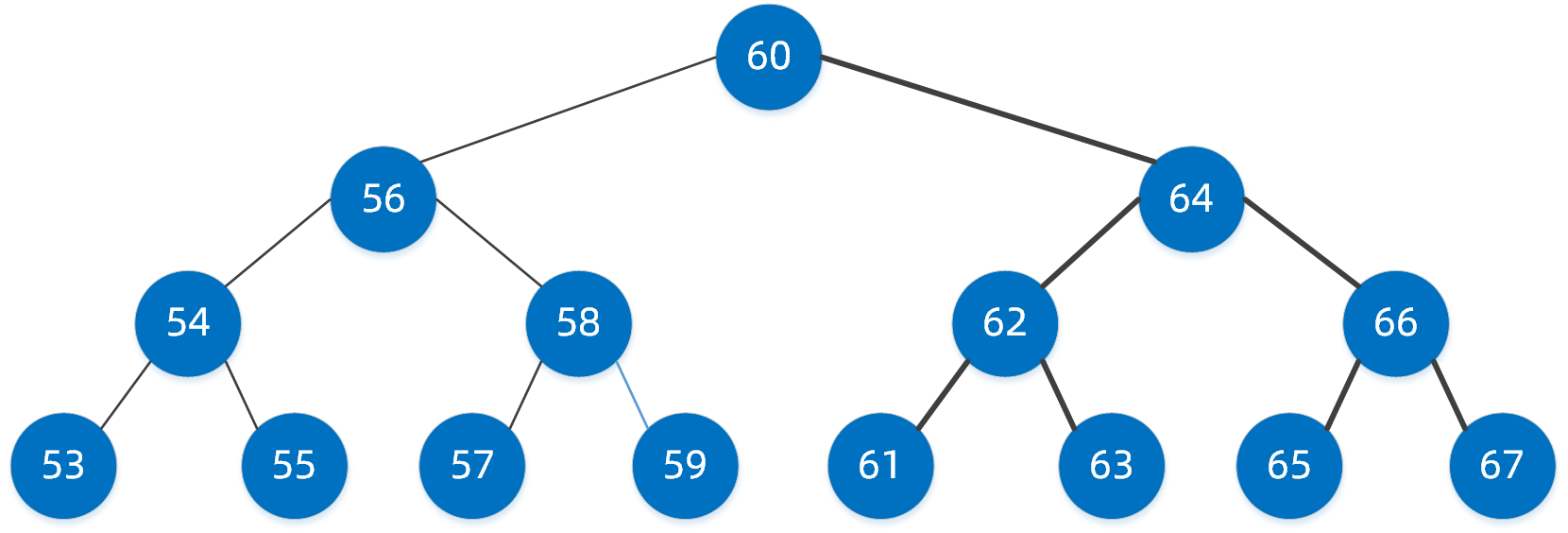
就是每个结点的值按照大小排列的二叉树，二叉查找树方便对结点的值进行查找

特点

• 节点的左子树小于节点本身；
• 节点的右子树大于节点本身；
• 左右子树同样为二叉搜索树；
• 没有相等的结点；

二叉查找树的查找操作

查找方式：

从根结点开始，如果要查找的数据等于结点的值， 那就返回。

如果要查找的数据小于结点的值，那就在左子树中递归查找；

如果要查找的数据大于结点的值，那就在右子树中递归查找。

红黑树

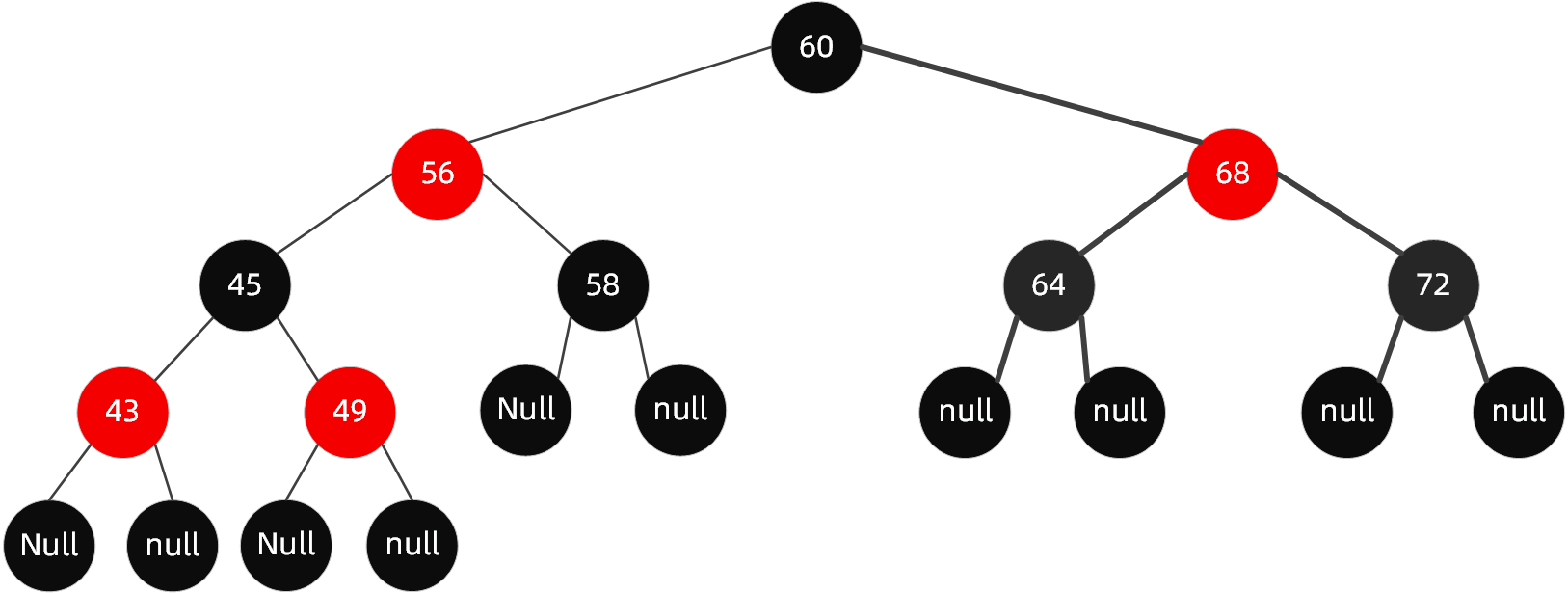
它可以在O(log n)时间内做查找，插入和删除，这里的n 是树中元素的数目

特点

• 每个节点都只能是红色或者黑色；
• 根节点必为黑色；
• 每个叶节点（NIL节点，空节点）是黑色的。
• 连接红色节点的两个子节点都为黑色（红黑树不会出现相邻的红色节点）；
• 从任意节点出发，到其每个叶子节点的路径中包含相同数量的黑色节点；
• 新加入到红黑树的节点为红色节点；

红黑树自平衡基本操作：

• 变色：在不违反上述红黑树规则特点情况下，将红黑树某个node节点颜色由红变黑，或者由黑变红；
• 左旋：逆时针旋转两个节点，让一个节点被其右子节点取代，而该节点成为右子节点的左子节点
• 右旋：顺时针旋转两个节点，让一个节点被其左子节点取代，而该节点成为左子节点的右子节点

红黑树的好处主要包括：

• 插入、删除和查找的时间复杂度最坏情况下为O(log n)，使得红黑树在时间敏感的应用如即时应用（real time application）中具有价值，同时也可以作为其他提供最坏情况担保的数据结构中的构建板块，例如，在计算几何中使用的很多数据结构都可以基于红黑树。
• 红黑树在函数式编程中也特别有用，是最常用的持久数据结构之一，它们用来构造关联数组和集合，在突变之后它们能保持为以前的版本。
• 红黑树是2-3-4树的一种等同，对于每个2-3-4树，都存在至少一个数据元素是同样次序的红黑树。在2-3-4树上的插入和删除操作也等同于在红黑树中颜色翻转和旋转。
• 与AVL树相比，红黑树在插入和删除时不需要维护绝对的平衡，旋转次数减少，可以提高效率。同时红黑树的平均查找效率还是log2（n）。

总之，红黑树具有较高的查找效率、插入和删除效率，同时对空间的使用效率也较高。

https://www.cnblogs.com/LiaHon/p/11203229.html