2023 CCPC 女生题解

gym

---

B. 终焉之茧 \(\star\)

显然两个维度分别做

单谷函数，起始点 \(A\) 是一个端点。一个 naive 的想法是三分目标点 \(B\)，但交互次数会超。二分关于 \(B\) 对称点 \(C\) 即可

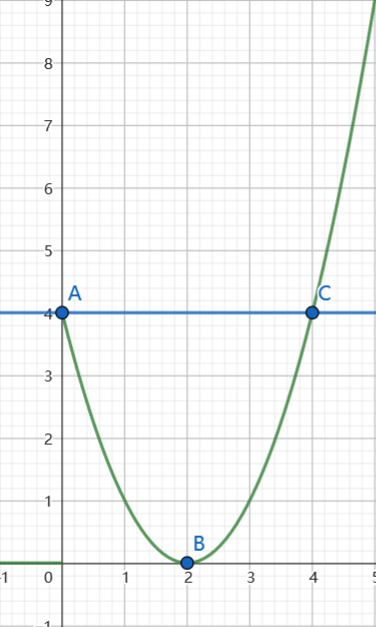
注意题目要求距离为 \(0\) 时立刻结束而不是最终距离为 \(0\)。一晚上没调出来

E. 永世乐土

key observation: 只需要记录没见过且没消失的英桀（只有它们对答案有贡献&受后续的侵蚀影响），所以每个英桀记忆体只有两种状态

设当前状态为 \((i,u,s)\)：走了 \(i\) 步（侵蚀了 \(i\) 个结点），位于结点 \(u\)，英桀状压为 \(s\)。转移枚举走到哪个结点和侵蚀哪个结点。记搜实现

时间复杂度 \(O(nmk2^{k})\)

F. 最长上升子序列 \(\star\)

有解的必要条件是前缀 \(\max\) 每次最多 \(+1\)，可以归纳证明也是充分条件

sol 1

\(a_{i}\) 相同的位置 \(p\) 一定是递减的。按 \(a_{i}\) 从小到大构造即可

sol 2

对于最大的 \(j<i\) 满足 \(a_{j}=a_{i}\) 有 \(p_{j}>p_{i}\)；对于最大的 \(k<i\) 满足 \(a_{k}+1=a_{i}\) 有 \(p_{k}<p_{i}\)。拓扑排序即可

H. 字符串游戏

题意：若 \(s_{i}=t[r-|s_{i}|+1,r]\)，则给答案贡献 \((r-|s_{i}|+1)(|t|-r+1)\)

\(r\) 可以枚举，前一个括号可以把 \(s_{i}\) 放到 AC 自动机上维护

J. 圣夜的奇迹跑者

先想办法把题读懂

如果一个技能发动了，我们只关心是否在完美位置发动，有效信息是在 \([1,R)\) 发动的概率（设为 \(p_{i}\)）

第 \(k\) 个技能在完美位置发动 \(\iff\) 至多提前发动 \(k-1\) 个且至少发动 \(k\) 个的最大概率。考虑算补集：至少发动 \(k\) 个的最大概率 \(-\) 至少提前发动 \(k\) 个的最小概率

注意到每个技能发动的概率相等而提前发动的不等，所以学习的技能一定是 \(p_{i}\) 最小的几个

按 \(p_{i}\) 升序排序。设 \(f[i,j]\) 表示学习了前 \(i\) 个技能，恰好发动了 \(j\) 个的概率，\(g[i,j]\) 为恰好提前发动 \(j\) 个的。转移：

\[f[i,j] = f[i-1,j-1]\times P + f[i-1,j]\times(1-P)
\]

\[g[i,j] = g[i-1,j-1]\times P\times p_{i}+g[i-1,j]\times(1-P\times p_{i})
\]

\(\displaystyle\sum_{j=k}^{i}f[i,j]-g[i,j]\) 即为学习前 \(i\) 个技能对 \(k\) 的答案

复杂度 \(O(n^{2})\)