WOE编码与IV值

参考:

WOE与IV值浅谈

 机器学习-变量筛选之IV值和WOE

0. Introduction

WOE (weight of evidence): 证据权重

IV (information value): 信息值

计算 WOE 与 IV 值的意义：

（1）用 woe 编码可以处理缺失值问题。

（2）IV值可以衡量各变量对 y 的预测能力，用于筛选变量。IV值越大，表示该变量的预测能力越强。

（3）对离散型变量，woe 可以观察组间的跳转对 odds 的提升是否呈线性，而 IV 可以衡量变量整体（而不是每个 group）的预测能力。

（4）对连续型变量，woe 和 IV 值为分箱的合理性提供了一定的依据。

1. WOE

1.1 WOE的计算方式

对于某变量，

\[WOE_i = ln(\frac{\#B_i/\#B_T}{\#G_i/\#G_T})， i=1,...,n(n为取值个数)
\]

其中 \(i\) 表示变量的第 \(i\) 个分箱（也即第 \(i\) 个取值），即一个变量的每个分箱都有一个 WOE 值，

\(\#B_i\) 是第 \(i\) 箱中坏客户（label=1）的人数

\(\#G_i\) 是第 \(i\) 箱中好客户（label=0）的人数

\(\#B_T\) 是总共坏客户人数

\(\#G_T\) 是总共好客户人数

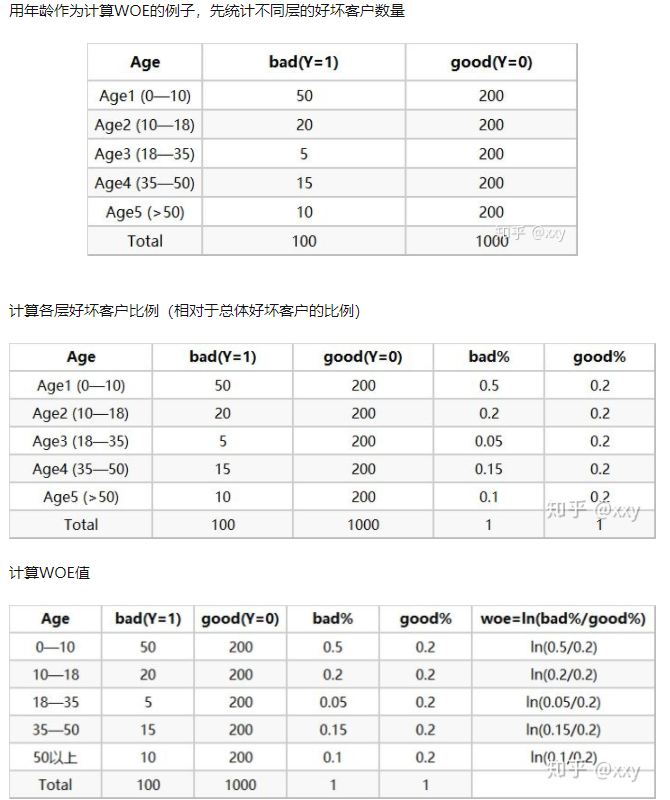
实质上WOE表示的是 当前分箱中好坏客户的比例 与 总体好坏客户比例 的差异

如果WOE的绝对值越大，这种差异就越明显，绝对值越小就表明差异越不明显。如果WOE为0，则说明该分箱中好坏客户比例等于随机好坏客户比值，此时这个分箱就无预测能力。

WOE 可以理解为当前组中正负样本的比值，与所有样本中正负样本比值的差异。这个差异是用这两个比值的比值，再取对数来表示的。

WOE>0表示当前组正负样本比例大于总体的正负样本比例，值越大表示这个分组里的样本响应的可能性越大；

WOE<0表示当前组正负样本比例小于总体的正负样本比例，值越小表示这个分组里的样本响应的可能性越小。

WOE绝对值越大，对于分类贡献越大。当分箱中正负的比例等于随机（大盘）正负样本的比值时，说明这个分箱没有预测能力，即WOE=0。

1.2 WOE编码的好处

逻辑回归假设

\[log(odds)=log(\frac{p}{1-p})=\theta_0+\theta_1x_1+...+\theta_px_p
\]

通常等式左边不会与等式右边呈线性关系，需要对 \(x\) 作变换 \(T(\cdot)\)，让 \(T(x)\) 与 \(log(odds)\) 线性相关。

（1）可以证明 WOE 是其中一种比较好的把自变量转化为与 \(log(odds)\) 线性相关的有效形式

（2）所有变量被 WOE 编码标准化后，求解得到的系数取值都在同一范围，可以直接比较不同自变量对 \(odds\) 的影响

1.3 对于连续型变量，如何进行WOE编码

在计算WOE编码前需要对连续型变量进行分箱（binning）处理，将其转化为离散型，再进行WOE编码。

1.3.1 分箱数量

一般来说10~20个分箱足够了，因为每个分箱应保证不少于5%的样本数。分箱数量决定了平滑程度，分箱数越少平滑度越高。所以一般采用先精细分箱（fine classing），初始将箱数分成20~50个箱，然后进行粗分箱（coarse classing），利用IV值、基尼系数、卡方统计量等值将箱数合并，通常最多10箱。目的是通过创建更少的箱子来实现简化，每个箱子具有明显不同的风险因子，同时最小化信息损失。

如果缺失值有预测能力，则将缺失值单独分作一箱或者是合并到拥有相似风险因子的分箱中去。

为什么不分1000箱？更少的箱数能够捕捉到数据中的重要模式，同时忽略噪声。当某一分箱中样本数少于5%，则该箱可能不是数据分布的一个真实反映，也可能导致模型不稳定。

1.3.2 处理分箱中没有响应样本或者全部是响应样本

可以用以下公式修正

\[WOE_i = ln(\frac{(\#B_i+0.5)/\#B_T}{(\#G_i+0.5)/\#G_T})
\]

1.3.3 如何用WOE检查分箱的正确性

（1）WOE最好应该呈单调趋势

（2）在预测变量做了WOE编码后跑一个单变量的逻辑回归，如果斜率（变量系数）不为1或者截距项不等于

\[\ln(\frac{\#Bad_T}{\#Good_T})
\]

则该分箱效果不佳。

对于离散变量，例如职业变量包含学生、老师、工人等名义属性时，先将变量的不同level作WOE编码后，把WOE值相近的level合并在一起，这样可以减少level数量。因为有相近的WOE值的level有几乎相同的响应率/非响应率，换句话说，某几个level有相近的woe值就将他们合并成一个箱子

1.4 WOE编码的优点与缺点

优点：

可以有效处理缺失值(把缺失值单独作为一个分箱)
可以有效处理异常值（Outlier）
WOE转换基于分布的对数值，这与逻辑回归输出函数一致
不需要进行哑变量编码
用了合适的分箱手段后，能够建立自变量与因变量的单调关系

缺点：

只考虑了每个分箱的相对风险，没有考虑到每个分箱样本数量占全样本的比例。可以用IV值来评估每个分箱的相对贡献

1.5 延申：WOE 为什么被称为数据权重

1.6 在python中计算WOE

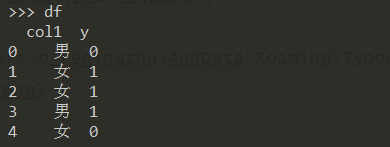
例：构造如下数据集

df = pd.DataFrame({"col1":["男","女","女","男","女"],

		"y":[0,1,1,1,0]})

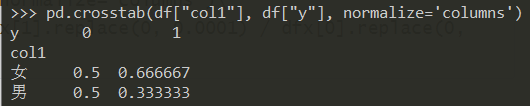
利用 crosstab 得到频率表：

pd.crosstab(df["col1"], df["y"], normalize='columns')

在频率表的基础上，加上woe列：

df_woe = pd.crosstab(df["col1"], df["y"], normalize='columns').\

assign(woe=lambda dfx: np.log(dfx[1].replace(0, 0.0001) / dfx[0].replace(0, 0.0001)))

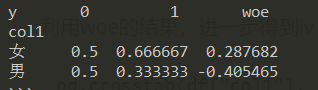
当某个分箱中，只存在正样本或负样本时，会使得 ln(.) 的分子或分母为0，可选择将其替换为0.0001

2. IV值

2.1 IV值的计算方式

信息值是预测模型中选择重要变量的方式之一，它能根据预测变量的重要性对预测变量进行排序，IV值计算公式如下：

\[IV = \sum_i^n(响应比例-未响应比例)*WOE_i \\
=\sum_i^n(\frac{\#Bad_i}{\#Bad_T}-\frac{\#Good_i}{\#Good_T})*WOE_i
\]

IV值是对一个变量而言，即每个变量有一个IV值（其值等于每个分箱的IV值相加）。IV值在WOE的基础上保证了结果非负。

假设变量 \(X\) 有 \(n\) 个分箱，每个分箱的 WOE 编码取值为 \(WOE_i\) ，该分箱的IV值就是用该分箱响应比例与未响应比例之差再乘上 \(WOE_i\)。注意这里的响应比例和未响应比例都是用当前分箱中响应数量/整体样本响应数量和当前分箱未响应数量/整体样本未响应数量计算得到。

IV值是看单个变量正负样本分布的差异，这种差异越大表明这个变量对于正负样本的区分度越高.

WOE可能为负值，IV值不可能为负，根据IV值选择变量后，用WOE替换变量各分组的值进入模型。

2.2 利用IV值进行变量筛选

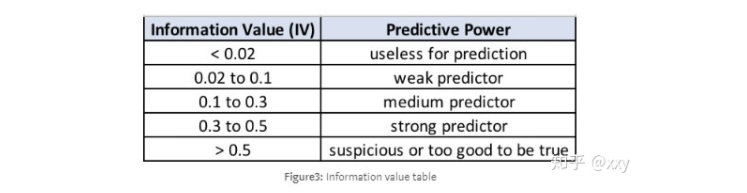
一般我们选择 IV值大于0.02的那些变量进入模型。如果IV值大于0.5，则考虑要对这个变量进行分群处理。即根据这个变量拆分成几个样本子集，分别在各个样本子集上建模。

2.3 在python中计算IV

def calIV(df, var, y):

    """

    计算IV值

    param df：数据集X

    param var：已分组的列名

    param y：响应变量y（0,1）

    return：IV值

    """

    df_woe_iv = pd.crosstab(df[var], y, normalize='columns').assign(woe=lambda dfx: np.log(dfx[1].replace(0, 0.0001) / dfx[0].replace(0, 0.0001))).assign(iv=lambda dfx: np.sum(dfx['woe'] * (dfx[1] - dfx[0])))

    a = df_woe_iv['iv'].reset_index()

    return a.loc[0, 'iv']