HDU-2571命运

Problem Description

穿过幽谷意味着离大魔王lemon已经无限接近了！
可谁能想到，yifenfei在斩杀了一些虾兵蟹将后，却再次面临命运大迷宫的考验，这是魔王lemon设下的又一个机关。要知道，不论何人，若在迷宫中被困1小时以上，则必死无疑！
可怜的yifenfei为了去救MM，义无返顾地跳进了迷宫。让我们一起帮帮执着的他吧！
命运大迷宫可以看成是一个两维的方格阵列，如下图所示：

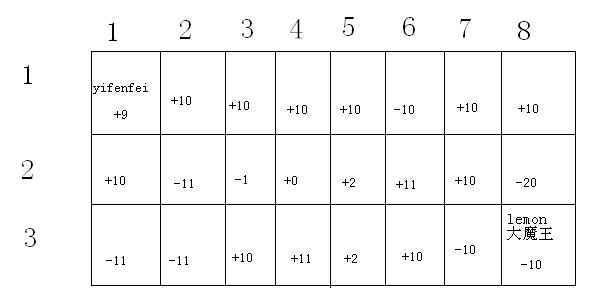
yifenfei一开始在左上角，目的当然是到达右下角的大魔王所在地。迷宫的每一个格子都受到幸运女神眷恋或者痛苦魔王的诅咒，所以每个格子都对应一个值，走到那里便自动得到了对应的值。
现在规定yifenfei只能向右或者向下走，向下一次只能走一格。但是如果向右走，则每次可以走一格或者走到该行的列数是当前所在列数倍数的格子，即：如果当前格子是（x,y），下一步可以是（x+1,y），(x,y+1)或者(x,y*k) 其中k>1。
为了能够最大把握的消灭魔王lemon，yifenfei希望能够在这个命运大迷宫中得到最大的幸运值。

 

Input

输入数据首先是一个整数C，表示测试数据的组数。
每组测试数据的第一行是两个整数n,m，分别表示行数和列数(1<=n<=20,10<=m<=1000)；
接着是n行数据，每行包含m个整数，表示n行m列的格子对应的幸运值K ( |k|<100 )。

 

Output

请对应每组测试数据输出一个整数，表示yifenfei可以得到的最大幸运值。

 

Sample Input

1
3 8
9 10 10 10 10 -10 10 10
10 -11 -1 0 2 11 10 -20
-11 -11 10 11 2 10 -10 -10

 

Sample Output

52

---

思路：

简单经典的DP

对于要被DP的元素，线性的或者二维表，我们是从头扫到尾的，这个顺序是从前往后的是为了给后面的点做铺垫，但是对于每一次的扫描，我们是要刷新已有的那些点，这时候只有向前看才能真正的实现“做铺垫”。

对于这题而言，每一次的扫描，我们从可能从dp[i-1][j],dp[i][j-1],dp[i][j/k]这些可能的点中取得最大的值，然后更新当前的点

有一点要注意的是为了良好的拓展性，我们要将第一行和第一列都纳入到for循环中去，而这样的做的前提是把第0行和第0列都置为-INF

想明白了一个问题，就是在一开始的时候为什么要把dp[0][1]和dp[1][0]都设置为0，是为了让dp[1][1]在for循环中能求得正确的答案，我们也可以直接手动的设置它的初始值。对于这些特殊的值（第一行，第一列），我们要单独的拿出来考虑，即如果考虑到特殊值的同时也考虑到了扩展性，我们就要仔细的设置好默认值。

---

#include <iostream>
#include <cstring>
#define MAX 1007
#define INF 65535
#define max(a,b) (a)>(b)?(a):(b)
using namespace std;

int G[][MAX];
int dp[][MAX];

int main()
{
    int n,m;
    int T;
    cin>>T;
    while(T--)
    {
        cin>>n>>m;
        for(int i = ;i <= n;i++)
            for(int j = ;j <= m;j++) {
                cin>>G[i][j];
                dp[i][j] = -INF;
            }
        for(int i = ;i <= m;i++)
            dp[][i] = -INF;
        for(int i = ;i <= n;i++)
            dp[i][] = -INF;
        dp[][]=dp[][]=;
        //dp[1][1] = G[1][1];
        for(int i = ;i <= n;i++)
            for(int j = ;j <= m;j++) {
                dp[i][j] = max(dp[i-][j],dp[i][j-]);
                for(int k = ;k <= m;k++) {
                    if(j%k==)
                        dp[i][j] = max(dp[i][j],dp[i][j/k]);
                }
                dp[i][j] += G[i][j];
            }
        cout<<dp[n][m]<<endl;
    }
    return ;
}