最短路问题：迪杰斯特拉算法（Dijsktra）

Dijkstra算法

1.定义概览

Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法，用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。Dijkstra算法是很有代表性的最短路径算法，在很多专业课程中都作为基本内容有详细的介绍，如数据结构，图论，运筹学等等。注意该算法要求图中不存在负权边。(只能用来计算起点只有一个的算法)

问题描述：在无向图 G=(V,E) 中，假设每条边 E[i] 的长度为 w[i]，找到由顶点 V0 到其余各点的最短路径。（单源最短路径）

2.算法描述

1)算法思想：设G=(V,E)是一个带权有向图，把图中顶点集合V分成两组，第一组为已求出最短路径的顶点集合（用S表示，初始时S中只有一个源点，以后每求得一条最短路径 , 就将加入到集合S中，直到全部顶点都加入到S中，算法就结束了），第二组为其余未确定最短路径的顶点集合（用U表示），按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中，总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。此外，每个顶点对应一个距离，S中的顶点的距离就是从v到此顶点的最短路径长度，U中的顶点的距离，是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。

2)算法步骤：

a.初始时，S只包含源点，即S＝{v}，v的距离为0。U包含除v外的其他顶点，即:U={其余顶点}，若v与U中顶点u有边，则<u,v>正常有权值，若u不是v的出边邻接点，则<u,v>权值为∞。

b.从U中选取一个距离v最小的顶点k，把k，加入S中（该选定的距离就是v到k的最短路径长度）。

c.以k为新考虑的中间点，修改U中各顶点的距离；若从源点v到顶点u的距离（经过顶点k）比原来距离（不经过顶点k）短，则修改顶点u的距离值，修改后的距离值的顶点k的距离加上边上的权。

d.重复步骤b和c直到所有顶点都包含在S中。

4.算法实例

先给出一个无向图

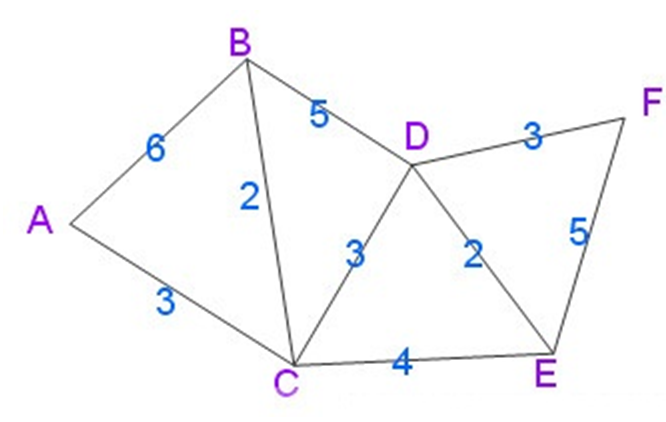
用Dijkstra算法找出以A为起点的单源最短路径步骤如下

下面附上代码实现：

//以下只是Dijsktra的函数！！！
int dijkstra(int n)
{
    //初始化v[0]到v[i]的距离
    ;i<=n;i++)
        dis[i] = w[][i];
    vis[]=;//标记v[0]点
    ; i <= n; i++)
    {
        //查找最近点
        ;
        ; j <= n; j++)
            if(!vis[w] && dis[j] < min)
                min = dis[w],k = j;
        vis[k] = ;//标记查找到的最近点
        //判断是直接v[0]连接v[j]短，还是经过v[k]连接v[j]更短
        ; j <= n; j++)
            if(!vis[j] && min+w[k][j] < dis[j])
                d[j] = min+w[k][j];
    }
    return dis[j];
}