一个小时，200行代码，手写Spring的IOC、DI、MVC

一、概述

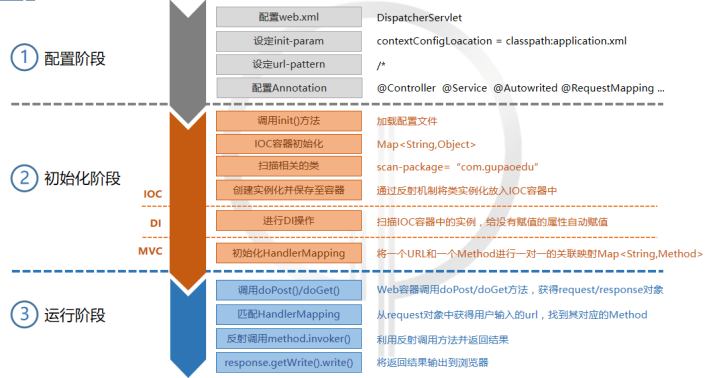
配置阶段：主要是完成application.xml配置和Annotation配置。

初始化阶段：主要是加载并解析配置信息，然后，初始化IOC容器，完成容器的DI操作，已经完成HandlerMapping的初始化。

运行阶段：主要是完成Spring容器启动以后，完成用户请求的内部调度，并返回响应结果。

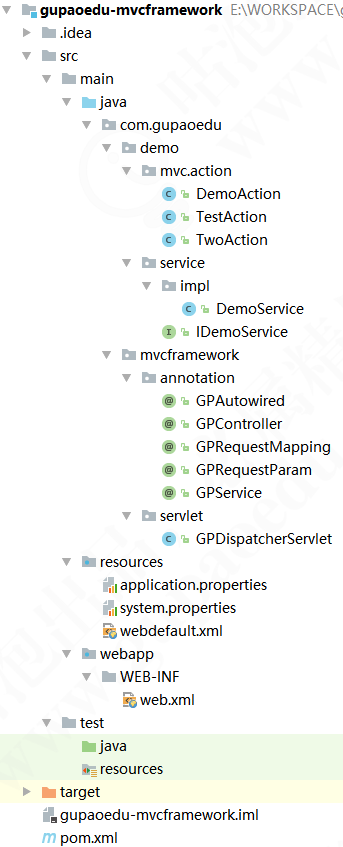
 二、配置

1、pom内部只使用servlet作为依赖

2、创建GPDispatcherServlet类继承HTTPServlet，重写init、doGet（调用后者）和doPost

3、web.xml配置servlet类以及初始化参数，即Spring的配置文件contextConfigLoaction=application.properties（内部配置扫描的包）

3、配置注解service、controller（本质是接口）以及元注解

4、可以进行测试-resp.getWriter().write(xxx)

三、初始化阶段

1、声明所需的成员变量---IOC<S,O>，urlde handlerMapping<S,M>

2、init方法实现：加载配置、扫描相关的类、初始化类实例并保存到ioc容器、依赖注入、构造handlerMapping

3、doLoadConfig()

4、doScanner()：递归扫描类文件

5、doInstance()：对类初始化并放至容器

6、doAutowired()：DI操作，将需要赋值的字段赋值

7、initHandlerMapping()：映射，将url和方法关联

四、运行阶段

1、doPost内部调用doDispatch

2、doDispatch()：获取参数列表，，初始化类，根据url，利用反射机制，调用方法

参考资料：https://gper.club/articles/7e7e7f7ff0g52gce

录播链接：https://pan.baidu.com/s/1YGJ5xFVIWYjalHdwwipxlg

提取码：CSDN