跟我学算法-SVM(支持向量机)

支持向量机是一个点离决策边界越近，离决策面越远的问题

求解的过程主要是通过拉格朗日乘子法，来求解带约束的优化问题，在问题中涉及两个方面，一个是线性的，一个是非线性的，非线性的有

我们平时比较常见的高斯核函数(径向基函数),他的主要做法就是把低维的数据变成高维数据，通过^2的方法

在支持向量基中的参数有 svc__C(松弛因子)和svc__gamma 两个参数,两个参数越大，模型的复杂度也越大

接下来我们使用一组人脸数据来进行模型，我们会进行参数调节

第一步数据载入

from sklearn.datasets import fetch_lfw_people  #从datasets数据包中获取数据
import pandas as pd
import matplotlib.pyplot as plt
faces = fetch_lfw_people(min_faces_per_person=60) #不小于60张图片
print(faces.target_names) #输出照片里的人物名字
print(faces.images.shape) #输出照片的大小, 639张， 62*47表示的是像素点，每个像素点代表的是一个数据

第二步 取前15张图片，画成3行5列的图片

fig, ax = plt.subplots(3, 5)
for i, axi in enumerate(ax.flat):
    axi.imshow(faces.images[i], cmap='bone') # cmap 表示配色方案,bone表示苍白的
    axi.set(xticks=[], yticks=[], xlabel=faces.target_names[faces.target[i]])  #faces.target[i]对应着0和1标签，
    # target_names 的 key 是 0和1...，value是名字
plt.show()

第三步：通过make_pipeline 连接pca，svm函数

from sklearn.svm import  SVC
from sklearn.decomposition import PCA
from sklearn.pipeline import make_pipeline

pca = PCA(n_components=150, whiten=True, random_state=42)  #whiten确保无相关的输出
svc = SVC(kernel='rbf', class_weight='balanced')  #核函数为径向基函数

model = make_pipeline(pca, svc)  #连接两个函数, 函数按照先后顺序执行

第四步: 通过GridSearchCV调节svc__C 和 svc__gamma 参数,.best_estimator获得训练好的模型

#把函数分为训练集和测试集
from sklearn.model_selection import train_test_split

Xtrain, Xtest, Ytrain, Ytest = train_test_split(faces.data, faces.target, random_state=40)

#参数调整svc__C和svc__gamma
from sklearn.model_selection import GridSearchCV

#备选参数
param_grid = {'svc__C':[1, 5, 10],
              'svc__gamma':[0.0001, 0.0005, 0.001]}

grid = GridSearchCV(model, param_grid) #第一个参数是model(模型)， 第二个参数是param_grid 需要调整的参数
print(Xtrain.shape, Ytrain.shape)
grid.fit(Xtrain, Ytrain) #建立模型
print(grid.best_params_) #输出模型的参数组合

model = grid.best_estimator_  #输出最好的模型

yfit = model.predict(Xtest)  #用当前最好的模型做预测

第五步：对预测结果画图，这里画了4*6的图

fig , ax = plt.subplots(4, 6)  #画出24副图，呈现4行6列的摆放形式

for i, axi in enumerate(ax.flat):
    axi.imshow(Xtest[i].reshape(62, 47), cmap='bone')
    axi.set(xticks=[], yticks=[])
    axi.set_ylabel(faces.target_names[yfit[i]].split()[-1],   #取名字的后一个字符，如果预测结果与真实结果相同，贤黑色，否则显红色
              color='black'if yfit[i]==Ytest[i] else 'red')

plt.show()
fig.suptitle('Predicted Names; Incorrect Labels in Red', size=14)  #加上标题

from sklearn.metrics import classification_report   #输出精确度，召回值
print(classification_report(Ytest, yfit, target_names=faces.target_names))

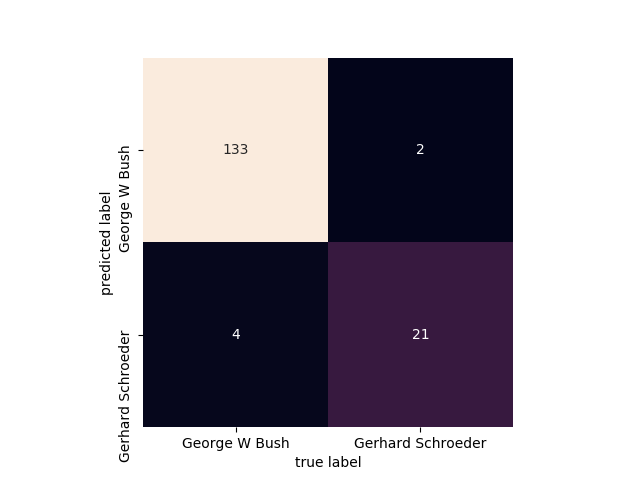
第六步：画出一个混淆矩阵的图

from sklearn.metrics import  confusion_matrix  #做混淆矩阵
import seaborn as sns
mat = confusion_matrix(Ytest, yfit)   #Ytest表示待测标签， yfit表示预测结果

sns.heatmap(mat.T, square=True, annot=True, fmt='d', cbar=False,

            xticklabels=faces.target_names,
            yticklabels=faces.target_names)
plt.xlabel('true label')
plt.ylabel('predicted label')
plt.show()