[CF544D]Destroying Roads_最短路_bfs

D. Destroying Roads

题目大意：

In some country there are exactly n cities and m bidirectional roads connecting the cities. Cities are numbered with integers from 1 to n. If cities a and b are connected by a road, then in an hour you can go along this road either from city a to city b, or from city b to city a. The road network is such that from any city you can get to any other one by moving along the roads.

You want to destroy the largest possible number of roads in the country so that the remaining roads would allow you to get from city s₁ to city t₁ in at most l₁ hours and get from city s₂ to city t₂ in at most l₂ hours.

Determine what maximum number of roads you need to destroy in order to meet the condition of your plan. If it is impossible to reach the desired result, print -1.

数据范围：

The first line contains two integers n, m (1 ≤ n ≤ 3000, 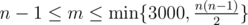) — the number of cities and roads in the country, respectively.

Next m lines contain the descriptions of the roads as pairs of integers a_i, b_i (1 ≤ a_i, b_i ≤ n, a_i ≠ b_i). It is guaranteed that the roads that are given in the description can transport you from any city to any other one. It is guaranteed that each pair of cities has at most one road between them.

The last two lines contains three integers each, s₁, t₁, l₁ and s₂, t₂, l₂, respectively (1 ≤ s_i, t_i ≤ n, 0 ≤ l_i ≤ n).

---

题解：

首先，保证了删掉的边最多，那就说明$s1$到$t1$和$s2$到$t2$都分别只有一条路径，不然的话我们还可以删掉更多的边。

接下来我们考虑，最终答案的形式。

必定是如下三种情况之一：

第一种，这两条路径互不相交。就是$s1$到$t1$，$s2$到$t2$。

第二种，存在一条公共路径，$l$到$r$，答案是$s1$到$l$，$l$到$r$，$r$到$t1$；和$s2$到$l$，$l$到$r$，$r$到$t2$。

最后一种是$s2$和$t2$调换，也就是$t2$到$l$，$l$到$r$，$r$到$s2$。

显然，每段路径都是最短路。

我们需要枚举$l$和$r$，也就是说我们需要多源最短路。

但是已知的算法最快也只能做到$n^2logn$，跑$n$遍堆优化$Dijkstra$。

好慢啊.....

诶，我们发现每条边的边权都相等，所以我们可以直接$bfs$。

因为边权都相等，所以每个点第一次到的时间戳就是距离。

然后枚举更新答案就好，不要忘记了第一种情况和判断是否超出了长度上限$l1$和$l2$。

代码：

#include <bits/stdc++.h>

#define N 3010 

using namespace std;

int head[N], to[N << 1], nxt[N << 1], tot;

int dis[N][N];

bool vis[N];

queue<int > q;

char *p1, *p2, buf[100000];

#define nc() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 100000,stdin), p1 == p2) ? EOF : *p1 ++ )

int rd() {
    int x = 0, f = 1;
    char c = nc();
    while (c < 48) {
        if (c == '-')
            f = -1;
        c = nc();
    }
    while (c > 47) {
        x = (((x << 2) + x) << 1) + (c ^ 48), c = nc();
    }
    return x * f;
}

inline void add(int x, int y) {
    to[ ++ tot] = y;
    nxt[tot] = head[x];
    head[x] = tot;
}

void bfs(int x) {
    while (!q.empty())
        q.pop();
    memset(dis[x], 0x3f, sizeof dis[x]);
    memset(vis, false, sizeof vis);
    vis[x] = true;
    dis[x][x] = 0;
    q.push(x);
    while (!q.empty()) {
        int p = q.front(); q.pop();
        for (int i = head[p]; i; i = nxt[i]) {
            if (!vis[to[i]]) {
                dis[x][to[i]] = dis[x][p] + 1;
                vis[to[i]] = true;
                q.push(to[i]);
            }
        }
    }
}

int main() {
    int n = rd(), m = rd();
    for (int i = 1; i <= m; i ++ ) {
        int x = rd(), y = rd();
        add(x, y), add(y, x);
    }
    int s1 = rd(), t1 = rd(), l1 = rd();
    int s2 = rd(), t2 = rd(), l2 = rd();
    for (int i = 1; i <= n; i ++ ) {
        bfs(i);
    }
    if(dis[s1][t1] > l1 || dis[s2][t2] > l2)
        puts("-1"), exit(0);
    int ans = dis[s1][t1] + dis[s2][t2];
    for (int i = 1; i <= n ; i ++ ) {
        for (int j = 1; j <= n; j ++ ) {
            int v1, v2;
            v1 = dis[s1][i] + dis[i][j] + dis[j][t1];
            v2 = dis[s2][i] + dis[i][j] + dis[j][t2];
            if(v1 <= l1 && v2 <= l2)
                ans = min(ans, v1 + v2 - dis[i][j]);
            v2 = dis[s2][j] + dis[j][i] + dis[i][t2];
            if(v1 <= l1 && v2 <= l2)
                ans = min(ans, v1 + v2 - dis[i][j]);
        }
    }
    printf("%d\n", m - ans);
    return 0;
}

小结：好题啊。对于一个没有思路的题，我们可以想一想最终答案的样子。如果有没有用上的条件，看看能不能通过那个条件来优化当前的不完美算法。