luogu P1494 [国家集训队]小Z的袜子 （ 普 通 ）

题目：    链接：https://www.luogu.org/problemnew/show/P1494

题意：一些袜子排成一排，每个袜子有固定的颜色。
                          每次询问在[l,r]的袜子中等概率选两只，求有多大的概率抽到两只一样颜色的。

思路： 其实 就是 求 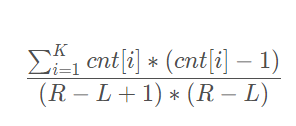    莫队维护 一波 cnt[ i ] * cnt[ i ]    就是模板嘛

#include<bits/stdc++.h>
#define LL long long
using namespace std;
int c[],pos[];
LL num[],up[],dw[],ans,u,v,w;
struct note {
    int l,r,id;
}a[];
bool cmp(note uu,note vv) {
    if(pos[uu.l]==pos[vv.l]) return uu.r<vv.r;
    return pos[uu.l]<pos[vv.l];
}
void updat(int x,int d) {
    ans-=num[c[x]]*num[c[x]];
    num[c[x]]+=d;
    ans+=num[c[x]]*num[c[x]];
}
int main() {
    int n,q;
    scanf("%d %d",&n,&q);
    int m=(int)sqrt(n);
    for(int i=;i<=n;i++) {
        scanf("%d",&c[i]);
        pos[i]=(i-)/m;
    }
    for(int i=;i<=q;i++) {
        scanf("%d %d",&a[i].l,&a[i].r); a[i].id=i;
    }
    sort(a+,a++q,cmp);
    int l=;int r=; ans=; memset(num,,sizeof(num));
    for(int i=;i<=q;i++) {
        int in=a[i].id;
        if(a[i].l==a[i].r) {
            up[in]=,dw[in]=; continue;
        }

        if(r<a[i].r) {
            for(int j=r+;j<=a[i].r;j++) updat(j,);
        }
        else {
            for(int j=r;j>a[i].r;j--) updat(j,-);
        }
        r=a[i].r;

        if(l<a[i].l) {
            for(int j=l;j<a[i].l;j++) updat(j,-);
        }
        else {
            for(int j=l-;j>=a[i].l;j--) updat(j,);
        }
        l=a[i].l;

        u=ans-a[i].r+a[i].l-;
        v=(LL)(a[i].r-a[i].l+)*(a[i].r-a[i].l);
        w=__gcd(u,v); u/=w; v/=w; up[in]=u; dw[in]=v;
    }
    for(int i=;i<=q;i++) printf("%lld/%lld\n",up[i],dw[i]);
    return ;
}