讲IOC非常好的一篇文章--初步弄懂DI

http://jinnianshilongnian.iteye.com/blog/1413846

http://jinnianshilongnian.iteye.com/blog/pdf

之后又看了类与类之间关系：

下面这篇文章是来自：

http://jinnianshilongnian.iteye.com/blog/1415277

类与类之间的关系-依赖，关联，聚合，组合，继承泛化的区别

1)依赖
依赖关系是类与类之间的联接。一个类依赖于另一个类的定义。如，一个人(Person)可以买车(Car)和房子(House),Person类依赖于Car和House的定义，因为Person引入了Car和House。与关联不同的是，Person类中没有Car和House的属性，Car和House的实例是以参量的方式传入到buy()方法中的。一般而言，依赖关系在Java语言中体现为局部变量，方法形参，或者对静态方法的调用。

2)关联
关联是类与类之间的联接，使一个类知道另一个类的属性和方法。关联可以是双向，也可以是单向的。一般使用成员变量来实现。

3)聚合
聚合是一种强的关联关系。是整体和个体之间的关系。例如，汽车类与引擎类，轮胎类之间的关系就是整体与个体之间的关系。与关联关系一样，聚合关系也是通过实例变量实现的。但是关联关系涉及的两个类在同一层次，而聚合关系中两个类处在不平等的层次上，一个代表整体，一个代表部分。

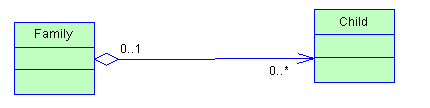
4)组合
组合也是关联关系的一种，一种比聚合关系强的关系。组合关系中的部分类不能独立于整体类存在。整体类和部分类有相同的生命周期。如Person类和Leg类。

5)继承/泛化
泛化和继承其实是一个逆过程 泛化就是有子类抽象出一个父类 而继承就是由父类具体化一个子类 例如足球比联赛跟什么西甲 意甲 英超之间就是泛化/继承的关系

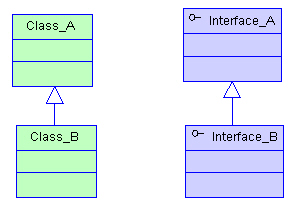
6)组合和聚合的区别
组合和聚合都属于关联，所以它们之间难免有相似之处，区别举例来说明：
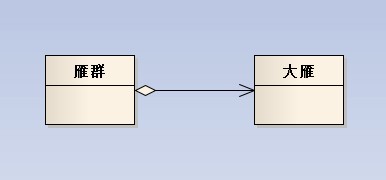
程老师的《大话》里举大那个大雁的例子很贴切 在此我就借用一下 大雁喜欢热闹害怕孤独 所以它们一直过着群居的生活 这样就有了雁群 每一只大雁都有自己的雁群 每个雁群都有好多大雁 大雁与雁群的这种关系就可以称之为聚合 另外每只大雁都有两只翅膀 大雁与雁翅的关系就叫做组合 有此可见 聚合的关系明显没有组合紧密 大雁不会因为它们的群主将雁群解散而无法生存 而雁翅就无法脱离大雁而单独生存——组合关系的类具有相同的生命周期
聚合关系图：

聚合关系图：

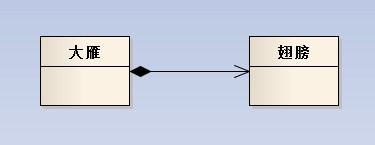
雁群类：

public class GooseGroup
{
    publi Goose goose;
    public GooseGroup(Goose goose){
        this.goose=goose;
    }
}

大雁类：

public class Goose{
    public Wings wings;
    public Goose()
    {
        wings=new Wings();
    }
}    

从构造函数来看，GooseGroup的构造函数要用到Goose作为参数把值传进来，Goose可以脱离GooseGroup独立存在。
组合关系中整体类含有部分类的实例化，Goose在实例化之前，一定要先实例化Wings，两个类紧密耦合在一起，它们有相同的生命周期，Wings不能独立于Goose存在。

从信息封装来看，聚合关系中，客户端同时了解GooseGroup和Goose，因为它们是独立的。
而在组合关系中，客户端只认识大雁类，根本不知道翅膀类的存在，因为翅膀类被严密封装在大雁类中。

 

分类: 架构