EOJ-3300 奇数统计（高维前缀和）

题目链接：

https://acm.ecnu.edu.cn/problem/3300/

题目大意：

给n个数，求在n个数中选两个数(可重复)，使得这两个数的组合数是奇数，求总共有多少种取法。

解题思路：

组合数C_n^m奇偶性判断：

n & m == m 成立则组合数为奇数

一开始没什么的思路，直接暴力超时，后来看到Lucas定理，发现上面那个式子的本质就是从这里推导出来的。

Lucas定理：

组合数判断奇数的话就是转化成上述定理中p = 2

是否为1，利用Lucas定理，先把和化为二进制，这样它们都是01序列了。我们又知道

。这样中为0的地方对应的中的位置只有一种可能，那就是0。

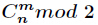
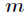
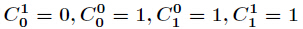
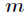
这样n&m = m的本质就是二进制中n对应的0得地方，m也对应为0。

然而，就是这个本质，就可以解这道题目

有位大佬一句话点醒了我，n&m = m说明m是n的子集。

对的，用二进制表示子集的时候，就是这样，m是n的子集，等价于n为0的位置m一定为0，n为1

的位置，m可以为1，可以为0。

然后对于每个n，求出它的子集的数目即可。

对于求子集，大佬教的方法是高维前缀和，代码很简单，就三行，和状态压缩DP一样。

 for(int i = ; i < m; i++)
 {
     for(int j = ; j < (<<m); j++)
     {
         if(j & (<<i))
               sum[j] += sum[j ^ (<<i)];
     }
 }   

举个例子，sum[0101] = sum[0101] + sum[0100] + sum[0001] + sum[0000]

sum[i]就表示i二进制的所有子集的权值之和

对于组合数n & m == m　　m是n的子集，

先统计每个数出现的次数，然后对于每个数，统计它的子集的个数即可，最后答案相加。

 #include<bits/stdc++.h>
 using namespace std;
 const int maxn = 1e6 + ;
 typedef long long ll;
 ll a[maxn], sum[maxn];
 int main()
 {
     int T, n, x;
     cin >> T;
     while(T--)
     {
         scanf("%d", &n);
         memset(a, , sizeof(a));
         memset(sum, , sizeof(sum));
         for(int i = ; i < n; i++)
         {
             scanf("%d", &a[i]);
             sum[a[i]]++;
         }
         int m = ;
         for(int i = ; i < m; i++)
         {
             for(int j = ; j < (<<m); j++)
             {
                 if(j & (<<i))
                     sum[j] += sum[j ^ (<<i)];
             }
         }
         ll ans = ;
         for(int i = ; i < n; i++)
             ans += sum[a[i]];
         cout<<ans<<endl;
     }
     return ;
 }