51Nod 最大子矩阵和 | DP

Input

第1行：M和N，中间用空格隔开（2 <= M,N <= 500)。
第2 - N + 1行：矩阵中的元素，每行M个数，中间用空格隔开。(-10^9 <= M[i] <= 10^9)

Output

输出和的最大值。如果所有数都是负数，就输出0。

Input示例

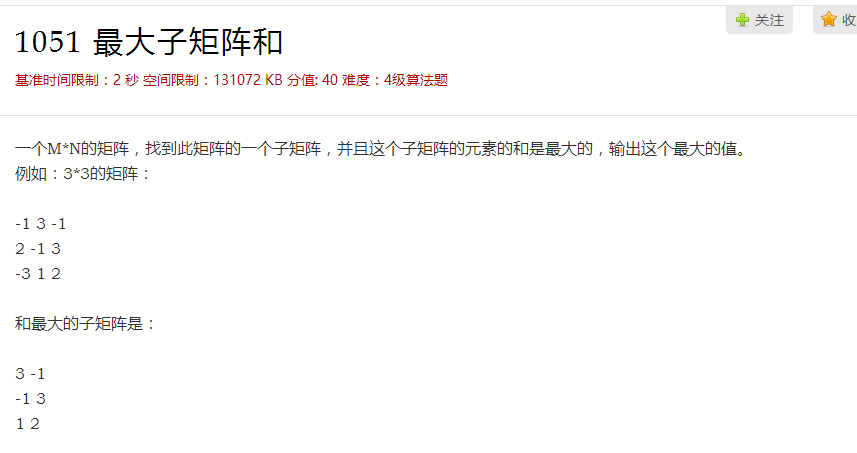
3 3
-1 3 -1
2 -1 3
-3 1 2

Output示例

7
 
用c[k]数组记录下i行到j行k列元素总和，得到的c数组是一行序列，我们通过（求最大子段和的方法）去线性处理算出值，（即i行到j行下矩阵的最大子矩阵）。 
c[k]

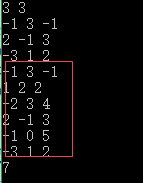
sum

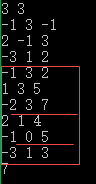
切三刀，切出一块

#include "bits/stdc++.h"
using namespace std;
#define rep(i, s, n) for(int i=s;i<n;i++)
#define _MOD 1000000007
#define ll long long
const int N=;
 
#define LL long long
#define INF 0x3f3f3f3f
#define PI acos(-1.0)
#define E 2.71828
#define MOD 1000000007
#define N 510
 
int p[N][N];
int c[N];
int main()
{
    int n,m;
    scanf("%d%d",&m,&n);
    for(int i = ; i < n; i++)
        for(int j = ; j < m; j++)
            scanf("%d",&p[i][j]);
    int ans = ;
    for(int i = ; i < n; i++)
    {
        for(int j = i; j < n; j++)
        {
            int maxn = ,sum = ;
            for(int k = ; k < m; k++)
            {
                c[k] = (j == i)?p[i][k] : (c[k] + p[j][k]);
                if(sum < )
                    sum = c[k];
                else
                    sum += c[k];
                if(maxn < sum)
                    maxn = sum;
            }
            if(ans < maxn)
                ans = maxn;
        }
    }
    printf("%d\n",ans);
    return ;
}

http://blog.csdn.net/qq_33199236/article/details/52717704