WebGL常用数学公式

1.三角函数

坐标轴采用右手法则，沿Z轴的逆时针方向为正角度，假设原始点为p(x,y,z),a是X轴旋转到点p的角度，r是从原始点到p点的距离。用这两个变量计算出点p的坐标，等式如下：

x = rcos a;
y = rsin a;

类似的可以使用r,a,b(p旋转的角度)来表示p'的坐标:

x' = r cos(a + b);
y' = r sin(a + b);

利用三角函数两角和公式：

sin(a +/- b) = sin a cos b +/- cos a sin b
cos(a +/- b) = cos a cos b -/+ sin a sin b

可得：

x' = r(cos a cos b - sin a sin b)
y' = r(sin a cos b + cos a sin b)

最后将x,y等式带入，消除r 和 a 可得等式：

x' = x cos b - y sin b
y' = x sin b + y cos b
z' = z

另外计算中也会用到弧度计算功能：

radian = a * (PI / 180)

2.变换矩阵：旋转

矩阵和矢量的方式可以用如下等式表示：

等式的右边由x、y、z组成的矢量被称为三维矢量。计算方式如下：

x' = ax + by + cz
y' = dx + ey + fz
z' = gx + hy + iz

在看看三角函数的等式,并与其比较：

x' = ax + by + cz
x' = x cosb - y sinb

如果 a = cosb, b = -sinb,c = 0,那么两个等式完全相同。在看y':

y' = dx + ey + fz
y' = x sinb + y cosb

如果 d = sinb, e = cobb, f = 0,那么两个等式完全相同。将这些结果代入到等式3.4中，得到等式：

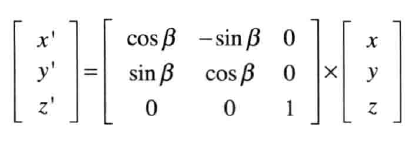
这个矩阵被称为变换矩阵（transformation matrix），也被称为旋转矩阵（rotation matrix）。

3.变换矩阵：平移

平移公式:x' = x + Tx。

如下所示是4*4矩阵：

该矩阵的乘法结果如下所示：

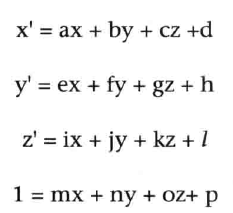
根据最后一个式子 1 = mx + ny + oz + p,很容易求得系数m = 0, n = 0, o = 0, p = 1;比较x',可知 a = 1, b = 0, c = 0, d = Tx;类似地，比较y'，可知e = 0, f = 1,g = 0, h = Ty；比较z'，可知i = 0, j = 0, k = 1, l = Tz。这样，就可以写出表示平移的矩阵，又称为平移矩阵（translation matrix）。如下所示：

4. 4*4的旋转矩阵

将旋转矩阵从一个3*3矩阵转变为一个4*4矩阵，只需要将旋转公式和4*4矩阵公式比较下:

x' = xcosb - ysinb
y' = xsinb + ycosb
z' = z
x' = ax + by + cz + d
y' = ex + fy + gz + h
z' = ix + jy + kz + l
l = mx + ny + oz + p

例如，当你通过比较x' = xcosb - ysinb与x' = ax + by +cz +d时，可知a = cosb, b = -sinb, c= 0, d = 0。以此类推，求得y'和z'等式中的系数，最终得到4*4的旋转矩阵。如下所示：

5.变换矩阵：缩放

假设在三个方向X轴，Y轴，Z轴的缩放因子Sx, Sy, Sz不相关，那么有：

x' = Sx * x
y' = Sy * y
z' = Sz * z

和矩阵的乘法结果比较，可知缩放操作的变换矩阵：

6.distance(position1, position2)

顶点着色器内置函数，计算出两个坐标之间的距离。参数：

position1:第一个坐标
    position2:第二个坐标
    返回距离，值为float类型

7.mix(x, y, z)函数（数学函数x*(1-z) + y*z）

GL_ES内置函数，该函数会计算x*(1-z) + y*z，其中x、y、z分别为第1、2和3个参数。