最小生成树-kruskal

kruskal算法,没有进行算法复杂度分析

判断俩个结点是否在同一个树上使用了dfs,比较low的写法

输入数据

//第一行,结点数,结点数,边数

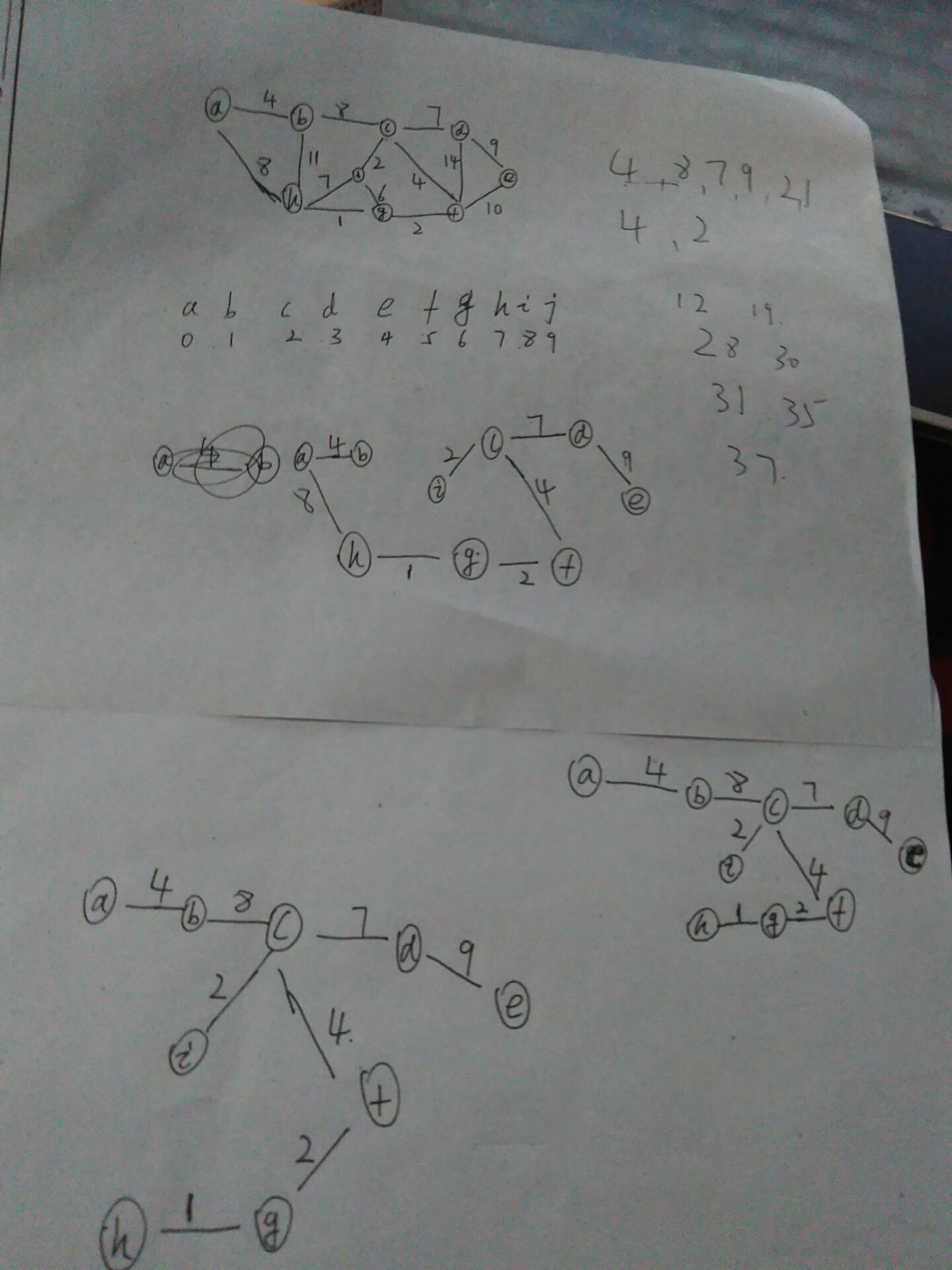
9 9 14
a b 4
b c 8
c d 7
a h 8
b h 11
h i 7
i c 2
i g 6
c f 4
d f 14
d e 9
f e 10
g h 1
g f 2

//============================================================================
// Name        : kruskal.cpp
// Author      : caicai
// Version     :
//============================================================================

#include <iostream>
#include <stdio.h>
#include <memory.h>
using namespace std;

struct Node
{
	char s;
	char e;
	int w;
};

void printMap(int r, int a[][100])
{
	for(int i = 0; i < r; i++)
	{
		for(int j = 0; j < r; j++)
		{
			printf("%-3d", a[i][j]);
		}
		cout << endl;
	}
	cout << endl;
}
/**
 * 边根据权重从小到大排序
 */
void sortEdge(Node edges[], int total)
{
	Node temp;
	for(int i = 0; i < total; i++)
	{
		for(int j = 1; j < total; j++)
		{
			if(edges[j - 1].w > edges[j].w)
			{
				temp = edges[j - 1];
				edges[j - 1] = edges[j];
				edges[j] = temp;
			}
		}
	}
}
void printEdges(Node edges[], int total)
{
	for(int i = 0; i < total; i++)
		cout << edges[i].s << " " << edges[i].e << " " << edges[i].w << endl;
}
void dfs(int a[][100], int r, int s, int e, int* ok, int vis[])
{
	for(int i = 0; i < r; i++)
	{
		if(vis[i] || a[s][i] == 0)
		{
			//走过,不存在的路
			continue;
		}
		if(i == e)
		{
			//可到
			*ok = 0;
			return;
		}
		vis[i] = 1;
		//从当前结点出发,不需要回溯,如果当前结点到不了,从其他结点到当前结点同样是到不了
		dfs(a, r, i, e, ok, vis);
	}
}
void kruskal(int a[][100], int r, Node edges[], int et)
{
	/**
	 * 图G n个结点,刚开始每一个结点都一个单独的结点,并没有与任何结点连接
	 * 将边按照权值从小到大排序
	 * 循环边集合,检查该边连接的俩个点,是否在同一个树上,如果是,不要,如果不是,加入到最小生成树中
	 * 怎么检查,a到b是否有一个条路
	 * 检查是否在同一个树中,dfs检查
	 */
	/*
	 *1初始化:生成的树为空,总权值为0
	 *2循环:每一次循环边,加入到数组a,数组a中包含n棵树,对于每一颗树,加入的边的权值最小,所以加入此边后形成的树的总权也是最小的
	 *     当俩棵树合并时,每棵的树的总权值也是最小的,所以相加后总权也是最小
	 *3终止:每一次加入的边是权值也是最小的,所以循环终止时,总权也是最小的
	 */
	for(int i = 0; i < et; i++)
	{
		char s = edges[i].s;
		char e = edges[i].e;
		int ok = 1;
		int vis[100];
		memset(vis, 0, sizeof(vis));
		//检查耗时
		dfs(a, r, s - 'a', e - 'a', &ok, vis);
		if(ok)
		{
			//不在同一颗树中,当前的边加入到树中
			a[s - 'a'][e - 'a'] = edges[i].w;
			//无向图
			a[e - 'a'][s - 'a'] = edges[i].w;
		}
	}
}
int main()
{
	freopen("d:\\2.txt", "r", stdin);
	int r;
	int te;
	cin >> r >> r >> te;
	char s, e;
	int w;
	int a[100][100];
	Node edges[100];
	int et = 0;
	while (te--)
	{
		cin >> s >> e >> w;
		//cout << s << " " << e << " " << w << endl;
		Node node;
		node.s = s;
		node.e = e;
		node.w = w;
		edges[et++] = node;
	}
	sortEdge(edges, et);
	printEdges(edges, et);
	kruskal(a, r, edges, et);
	printMap(r, a);
	return 0;
}

　　输出

g h 1
i c 2
g f 2
a b 4
c f 4
i g 6
c d 7
h i 7
b c 8
a h 8
d e 9
f e 10
b h 11
d f 14
0  4  0  0  0  0  0  0  0
4  0  8  0  0  0  0  0  0
0  8  0  7  0  4  0  0  2
0  0  7  0  9  0  0  0  0
0  0  0  9  0  0  0  0  0
0  0  4  0  0  0  2  0  0
0  0  0  0  0  2  0  1  0
0  0  0  0  0  0  1  0  0
0  0  2  0  0  0  0  0  0