[NOIP2016PJ]魔法阵

今天模拟赛的题，，，唯一没有Giao出来的题（不然我就AKIOI了~）

最开始没想到数学题，把所有部分分都说一遍吧：

35分：纯暴力O(M^4)枚举，对于每一组a,b,c,d验证其是否合法。

60分：经过读题，不难发现a,b,c,d单调递增，可以考虑对其进行排序后再暴力枚举，枚举量减少近一半。

85分：对xb-xa=2(xd-xc)进行分析，可以得到以下公式：double((xb-xa+2xc)/2)=double(xd)，再查找是否存在xd，这样我们只需枚举a,b,c，时间复杂度是O(M^3)

100分：依旧是对xb-xa=2(xd-xc)进行分析，我们设t=xd-xc，则xb-xa=2⋅t；再分析第二个条件Xb−Xa<(Xc−Xb)/3，我们可以得到Xc−Xb>6⋅t，我们给他补全成等号，就是Xc−Xb=6⋅t+k

所以这四个数在数轴上的排列如图所示（图片来自博客园）

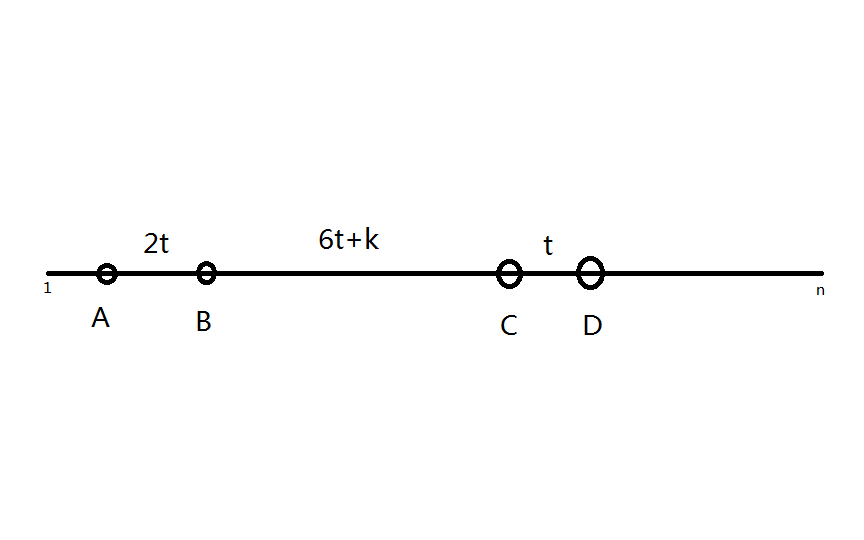
所以我们会有一个不成熟的思路：在1-n/9范围内枚举t，把a,b,c,d拿t表示出来。

那么如何计算呢？枚举D。当我们枚举到一个D值的时候，与之对应的C值是确定的（不受k影响），而A值和B值却不一定。因此我们可以找到最大的与之对应的A值B值。

但是有可能会存在一组AB值要比当前计算到的小，怎么办呢？不妨设有可能存在的比最大值小的A值为A1，B值为B1，计算到的为A2和B2

当A1<A2&&B1<B2时，只要A2和B2能组成魔法阵，A1和B1一定可以（k只是大于0的数，而对k的上界没有限制，当我们把k放大时，就可以构造出A1和B1了）。

由于是顺序枚举，所以我们可以记录一下之前有多少组合法解（类似于前缀和），最后再用乘法原理计算。同样的方法，我们从A的上界往A的下界枚举记录后缀和然后计算即可。

下面给出参考代码：

 // luogu-judger-enable-o2
 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #define N 50005
 #define M 50005
 using namespace std;
 int n,m,ans[M][],num[M],a[M],A,B,C,D;
 int read()
 {
     int x=,f=;char ch=getchar();
     while(ch<''||ch>''){if(ch=='-')f=;ch=getchar();}
     while(ch>=''&&ch<=''){x=(x<<)+(x<<)+(ch^);ch=getchar();}
     if(f)return x;return -x;
 }
 int main()
 {
     n=read();m=read();
     for(int i=;i<=m;i++)
     {
         a[i]=read();
         num[a[i]]++;
     }
     for(int t=;t*<n;t++)
     {
         int sum=;
         for(D=*t+;D<=n;D++)
         {
             C=D-t;
             B=C-*t-;
             A=B-*t;
             sum+=num[A]*num[B];
             ans[C][]+=num[D]*sum;
             ans[D][]+=num[C]*sum;
         }
         sum=A=B=C=D=;
         for(A=n-t*-;A>=;A--)
         {
             B=A+*t;
             C=B+*t+;
             D=C+t;
             sum+=num[C]*num[D];
             ans[A][]+=num[B]*sum;
             ans[B][]+=num[A]*sum;
         }
     }
     for(int i=;i<=m;i++)
     {
         for(int j=;j<=;j++)
         {
             cout<<ans[a[i]][j]<<" ";
         }
         cout<<endl;
     }
     return ;
 }