poj 2187 Beauty Contest(平面最远点)

Beauty Contest

Time Limit: 3000MS		Memory Limit: 65536K
Total Submissions: 24431		Accepted: 7459

Description

Bessie, Farmer John's prize cow, has just won first place in a bovine beauty contest, earning the title 'Miss Cow World'. As a result, Bessie will make a tour of N (2 <= N <= 50,000) farms around the world in order to spread goodwill between farmers and their cows. For simplicity, the world will be represented as a two-dimensional plane, where each farm is located at a pair of integer coordinates (x,y), each having a value in the range -10,000 ... 10,000. No two farms share the same pair of coordinates. 
Even though Bessie travels directly in a straight line between pairs of farms, the distance between some farms can be quite large, so she wants to bring a suitcase full of hay with her so she has enough food to eat on each leg of her journey. Since Bessie refills her suitcase at every farm she visits, she wants to determine the maximum possible distance she might need to travel so she knows the size of suitcase she must bring.Help Bessie by computing the maximum distance among all pairs of farms. 

Input

* Line 1: A single integer, N 
* Lines 2..N+1: Two space-separated integers x and y specifying coordinate of each farm 

Output

* Line 1: A single integer that is the squared distance between the pair of farms that are farthest apart from each other. 

Sample Input

4
0 0
0 1
1 1
1 0

Sample Output

2

Hint

Farm 1 (0, 0) and farm 3 (1, 1) have the longest distance (square root of 2) 

Source

USACO 2003 Fall

 

 

 

旋转卡壳学习链接：

http://blog.csdn.net/ACMaker

 

 

 

想法：

总结起来，问题解决步骤为：

1、用Graham's Scanning求凸包

2、用Rotating Calipers求凸包直径，也就找到了最远点对。

该算法的平均复杂度为O(nlogn) 。最坏的情况下，如果这n个点本身就构成了一个凸包，时间复杂度为O(n^2)。 旋转卡壳可以用于求凸包的直径、宽度，两个不相交凸包间的最大距离和最小距离等。虽然算法的思想不难理解，但是实现起来真的很容易让人“卡壳”。

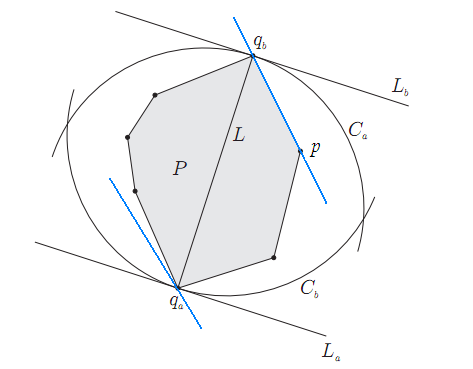
逆向思考，如果qa，qb是凸包上最远两点，必然可以分别过qa，qb画出一对平行线。通过旋转这对平行线，我们可以让它和凸包上的一条边重合,如图中蓝色直线，可以注意到，qa是凸包上离p和qb所在直线最远的点。于是我们的思路就是枚举凸包上的所有边，对每一条边找出凸包上离该边最远的顶点，计算这个顶点到该边两个端点的距离，并记录最大的值。直观上这是一个O(n2)的算法，和直接枚举任意两个顶点一样了。但是注意到当我们逆时针枚举边的时候，最远点的变化也是逆时针的，这样就可以不用从头计算最远点，而可以紧接着上一次的最远点继续计算，于是我们得到了O(n)的算法。

 #include <stdio.h>
 #include <string.h>
 #include <algorithm>
 #include <iostream>
 #include <math.h>
 using namespace std;

 struct Point
 {
     int x,y;
     Point(int _x = , int _y = )
     {
         x = _x;
         y = _y;
     }
     Point operator -(const Point &b)const
     {
         return Point(x - b.x, y - b.y);
     }
     int operator ^(const Point &b)const
     {
         return x*b.y - y*b.x;
     }
     int operator *(const Point &b)const
     {
         return x*b.x + y*b.y;
     }
     void input()
     {
         scanf("%d%d",&x,&y);
     }
 };
 int dist2(Point a,Point b)//距离的平方！！！attention！！
 {
     return (a-b)*(a-b);
 }
 const int MAXN = ;
 Point list[MAXN];
 int Stack[MAXN],top;
 bool _cmp(Point p1,Point p2)
 {
     int tmp = (p1-list[])^(p2-list[]);
     if(tmp > )return true;
     else if(tmp ==  && dist2(p1,list[]) <= dist2(p2,list[]))
         return true;
     else return false;
 }
 void Graham(int n)//求凸包
 {
     Point p0;
     int k = ;
     p0 = list[];
     for(int i = ;i < n;i++)
         if(p0.y > list[i].y || (p0.y == list[i].y && p0.x > list[i].x))
         {
             p0 = list[i];
             k = i;
         }
     swap(list[],list[k]);
     sort(list+,list+n,_cmp);
     if(n == )
     {
         top = ;
         Stack[] = ;
         return;
     }
     if(n == )
     {
         top = ;
         Stack[] = ;
         Stack[] = ;
         return;
     }
     Stack[] = ;
     Stack[] = ;
     top = ;
     for(int i = ;i < n;i++)
     {
         while(top >  && ((list[Stack[top-]]-list[Stack[top-]])^(list[i]-list[Stack[top-]])) <=  )
             top--;
         Stack[top++] = i;
     }
 }

 //旋转卡壳，求两点间距离平方的最大值
 int rotating_calipers(Point p[],int n)
 {
     int ans = ;
     Point v;
     int cur = ;
     for(int i = ;i < n;i++)
     {
         v = p[i]-p[(i+)%n];
         while((v^(p[(cur+)%n]-p[cur])) < )//寻找到国定边的最远的点 p[cur]，然后更新距离！！！
             cur = (cur+)%n;

         ans = max(ans,max(dist2(p[i],p[cur]),dist2(p[(i+)%n],p[(cur+)%n])));//这里其实可以记录最远点对的坐标！！
     }
     return ans;
 }
 Point p[MAXN];

 int main()
 {
     int n;
     while(scanf("%d",&n) == )
     {
         for(int i = ;i < n;i++)
             list[i].input();
         Graham(n);
         for(int i = ;i < top;i++)
         {
             p[i] = list[Stack[i]];
         }
         printf("%d\n",rotating_calipers(p,top)) ;
     }
     return ;
 }