【JZOJ3294】【BZOJ4417】【luoguP3990】超级跳马

description

---

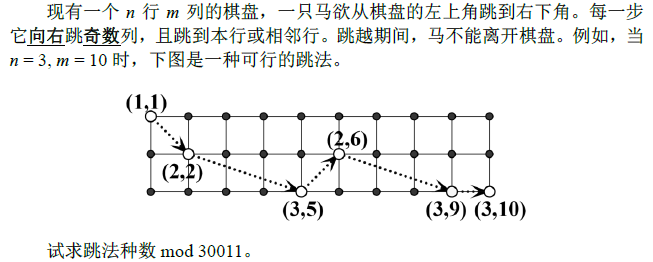
analysis

• 矩阵乘法好题

• 最朴素的\(10pts\)的\(f[i][j]\)容易\(DP\)，但是是\(O(nm^2)\)的复杂度

• 于是把\(10\)分的\(DP\)写出来，就可以知道\(f[i][j]+=f[k][l]\)的部分可以搞前缀和优化，\(O(nm)\)有\(50pts\)

• 这个要先弄懂才可以继续搞矩乘

• 可以分成奇数列和偶数列分别\(DP\)，设\(f[i],g[i]\)分别表示某奇数列的第\(i\)行和偶数列的第\(i\)行的方案数的前缀和

• \(f[i]\)和\(g[i]\)都要加上第\(i\)行前面与他奇偶性相同的方案数方便转移，具体见代码

• 于是\(f[i]=g[i-1]+g[i]+g[i+1],g[i]=f[i-1]+f[i]+f[i+1]\)（注意边界的两个点），可以矩乘优化了

• 具体就是，初始矩阵写成前一半是\(f[1..n]\)，后一半是\(g[1..n]\)

• 想办法矩乘转移到\((g[1..n],f’[1..n])\)，这里举\(n=3\)的例子

• \((1,0,0,1,1,0)*F=(1,1,0,3,2,1)\)，因为打表发现\(\left(
  \begin{matrix}
  1,1,2...\\
  0,1,2... \\
  0,0,1...
  \end{matrix}
  \right)\)，这个\(3\)加上了前面的那个\(1\)

• 于是由\((f[i-1],f[i],f[i+1],g[i-1],g[i],g[i+1])*F=(g[i-1],g[i],g[i+1],f’[i-1],f’[i],f’[i+1])\)推矩阵

• 注意\(f[i]=g[i-1]+g[i]+g[i+1]\)，推出来大概就是\(\left(
  \begin{matrix}
  0,0,0,1,0,0\\
  0,0,0,0,1,0 \\
  0,0,0,0,0,1\\
  1,0,0,1,1,0\\
  0,1,0,1,1,1\\
  0,0,1,0,1,1\\
  \end{matrix}
  \right)\)

• \(n=10\)的矩阵长这样

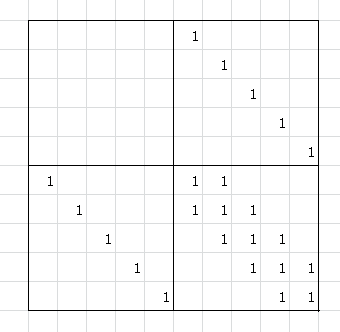
• 于是就可以直接上矩乘搞了，答案就为最后两位的和

---

code

#include<stdio.h>
#include<string.h>
#include<algorithm>
#define MAXN 55
#define mod 30011
#define ll long long
#define fo(i,a,b) for (ll i=a;i<=b;++i)
#define fd(i,a,b) for (ll ia=;i>=b;--i)

using namespace std;

ll n,m;

struct matrix
{
	ll a[MAXN<<1][MAXN<<1],n,m;
	matrix(){memset(a,0,sizeof(a)),n=m=0;}
	matrix(ll x,ll y){memset(a,0,sizeof(a)),n=x,m=y;}
}f,ans,ans1,f1;
inline ll read()
{
	ll x=0,f=1;char ch=getchar();
	while (ch<'0' || '9'<ch){if (ch=='-')f=-1;ch=getchar();}
	while ('0'<=ch && ch<='9')x=x*10+ch-'0',ch=getchar();
	return x*f;
}
inline matrix operator*(matrix a,matrix b)
{
	matrix c(a.n,b.m);
	fo(i,1,a.n)
	fo(j,1,b.m)
	fo(k,1,a.m)(c.a[i][j]+=a.a[i][k]*b.a[k][j])%=mod;
	return c;
}
inline matrix pow(matrix x,ll y)
{
	matrix z=x;
	while (y)
	{
		if (y&1)z=z*x;
		y>>=1,x=x*x;
	}
	return z;
}
int main()
{
	n=read(),m=read();
	ans=ans1=matrix(1,n<<1),f=f1=matrix(n<<1,n<<1);
	ans.a[1][1]=ans.a[1][n+1]=ans.a[1][n+2]=f.a[n+1][n+1]=1;
	fo(i,n+2,n<<1)f.a[i][i]=f.a[i-1][i]=f.a[i][i-1]=1;
	fo(i,1,n)f.a[i][n+i]=f.a[n+i][i]=1;
	f1=pow(f,m-3),ans1=ans*f1;
	printf("%lld\n",(ans1.a[1][n-1]+ans1.a[1][n])%mod);
	return 0;
}