NKOJ1472 警卫安排

P1472警卫安排

时间限制 : 10000 MS   空间限制 : 65536 KB

问题描述

一个重要的基地被分为n个连通的区域。出于某种神秘的原因，这些区域以一个区域为核心，呈一颗树形分布。
在每个区域安排警卫所需要的费用是不同的，而每个区域的警卫都可以望见其相邻的区域，只要一个区域被一个警卫望见或者是安排有警卫，这个区域就是安全的。你的任务是：在确保所有区域都是安全的情况下，找到安排警卫的最小费用。

输入格式

第一行n，表示树中结点的数目。
接下来的n行描述了n个区域的信息，每一行包含的整数依次为：区域的标号i(0<i<=n)，在区域i安排警卫的费用k，区域i的子结点数目m，接下来m个数为区域i的子结点编号。

输出格式

一行一个整数，为最小的安排费用。

样例输入

6
1 30 3 2 3 4
2 16 2 5 6
3 5 0
4 4 0
5 11 0
6 5 0

样例输出

25

提示

对于所有的数据，0<n<=720。

 

【题解】

“

“

——by 朱全民

 

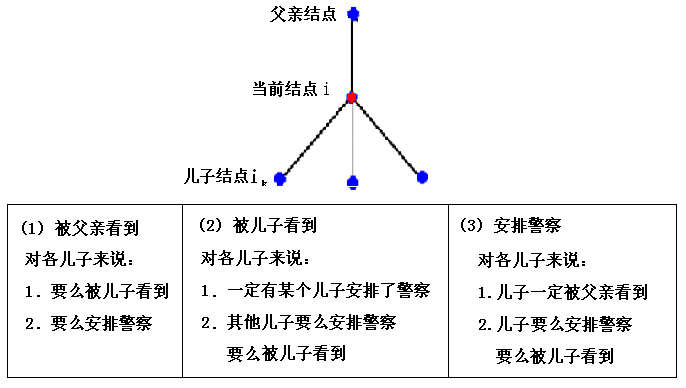
 #include <iostream>
 #include <cstdio>
 #include <cstdlib>
 #include <cstring>
 #include <cmath>
 #include <algorithm>
 #define min(a, b) ((a) < (b) ? (a) : (b))
 #define max(a, b) ((a) > (b) ? (a) : (b))

 inline void read(int &x)
 {
     x = ;char ch = getchar(), c = ch;
     while(ch < '' || ch > '')c = ch, ch = getchar();
     while(ch <= '' && ch >= '')x = x *  + ch - '', ch = getchar();
     if(c == '-')x = -x;
 }

 const int INF = 0x3f3f3f3f;
 const int MAXN =  + ;

 int n,cost[MAXN];

 struct Edge
 {
     int u,v,next;
     Edge(int _u, int _v, int _next){u = _u;v = _v;next = _next;}
     Edge(){}
 }edge[MAXN << ];

 int head[MAXN],cnt;

 inline void insert(int a, int b)
 {
     edge[++cnt] = Edge(a,b,head[a]);
     head[a] = cnt;
 }

 int fa[MAXN], dp[MAXN][];
 /*
 dp[i][0]表示i放警卫的最小费用
 dp[i][1]表示i被儿子看到的最小费用
 dp[i][2]表示i被父亲看到的最小费用 

 dp[i][0] = Σmin(dp[son[i]][2], dp[son[i]][0],dp[son[i][1]) + cost[i]
 dp[i][1] = Σmin(dp[son[i]][0], dp[son[i]][1]) + dp[j][0] j从son[i]中除去
 dp[i][2] = Σmin(dp[son[i]][1], dp[son[i]][2])
 */

 void dfs(int u)
 {
     if(!u)return;
     register int num = , v, cnt, tmp;//先更新0 2
     for(register int pos = head[u];pos;pos = edge[pos].next)
     {
         v = edge[pos].v;
         if(v == fa[u])continue;
         fa[v] = u;
         ++ num;
         dfs(v);
         dp[u][] += min(dp[v][], min(dp[v][], dp[v][]));
         dp[u][] += min(dp[v][], dp[v][]);
     }
     if(!num)
     {
         dp[u][] = cost[u];
         dp[u][] = INF;
         dp[u][] = ;
         return;
     }
     dp[u][] += cost[u];
     dp[u][] = INF;
     for(register int i = ;i <= num;++ i)
     {
         cnt = ;
         tmp = ;
         for(register int pos = head[u];pos;pos = edge[pos].next, ++ cnt)
         {
             v = edge[pos].v;
             if(v == fa[u])
             {
                 -- cnt;
                 continue;
             }
             if(cnt == i)tmp += dp[v][];
             else tmp += min(dp[v][], dp[v][]);
         }
         dp[u][] = min(dp[u][], tmp);
     }
 }

 int main()
 {
     read(n);
     register int root, tmp1,tmp2;
     for(register int i = ;i <= n;++ i)
     {
         read(root),read(cost[root]),read(tmp1);
         for(register int j = ;j <= tmp1;++ j)
         {
             read(tmp2);
             insert(root, tmp2),insert(tmp2, root);
         }
     }
     dfs(root);
     printf("%d", min(dp[root][], dp[root][]));
     return ;
 }

NKOJ