SPFA导读及介绍（转载)

适用范围：给定的图存在负权边，这时类似Dijkstra等算法便没有了用武之地，而Bellman-Ford算法的复杂度又过高，SPFA算法便派上用场了。 我们约定有向加权图G不存在负权回路，即最短路径一定存在。当然，我们可以在执行该算法前做一次拓扑排序，以判断是否存在负权回路，但这不是我们讨论的重点。

算法思想：我们用数组d记录每个结点的最短路径估计值，用邻接表来存储图G。我们采取的方法是动态逼近法：设立一个先进先出的队列用来保存待优化的结点，优化时每次取出队首结点u，并且用u点当前的最短路径估计值对离开u点所指向的结点v进行松弛操作，如果v点的最短路径估计值有所调整，且v点不在当前的队列中，就将v点放入队尾。这样不断从队列中取出结点来进行松弛操作，直至队列空为止

期望的时间复杂度O(ke)， 其中k为所有顶点进队的平均次数，可以证明k一般小于等于2。

实现方法：

　　建立一个队列，初始时队列里只有起始点，再建立一个表格记录起始点到所有点的最短路径（该表格的初始值要赋为极大值，该点到他本身的路径赋为0）。然后执行松弛操作，用队列里有的点作为起始点去刷新到所有点的最短路，如果刷新成功且被刷新点不在队列中则把该点加入到队列最后。重复执行直到队列为空。

判断有无负环：
　　如果某个点进入队列的次数超过N次则存在负环（SPFA无法处理带负环的图）

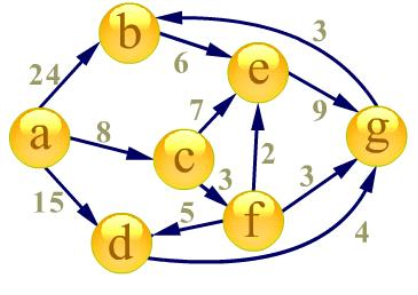
首先建立起始点a到其余各点的
最短路径表格

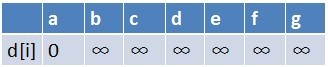
首先源点a入队，当队列非空时：
　１、队首元素（a）出队，对以a为起始点的所有边的终点依次进行松弛操作（此处有b,c,d三个点），此时路径表格状态为：

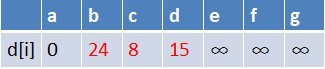
在松弛时三个点的最短路径估值变小了，而这些点队列中都没有出现，这些点
需要入队，此时，队列中新入队了三个结点b,c,d

队首元素b点出队，对以b为起始点的所有边的终点依次进行松弛操作（此处只有e点），此时路径表格状态为：

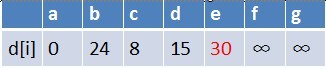
在最短路径表中，e的最短路径估值也变小了，e在队列中不存在，因此e也要
入队，此时队列中的元素为c，d，e

队首元素c点出队，对以c为起始点的所有边的终点依次进行松弛操作（此处有e,f两个点），此时路径表格状态为：

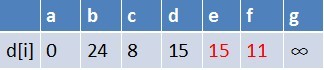
在最短路径表中，e，f的最短路径估值变小了，e在队列中存在，f不存在。因此
e不用入队了，f要入队，此时队列中的元素为d，e，f

队首元素d点出队，对以d为起始点的所有边的终点依次进行松弛操作（此处只有g这个点），此时路径表格状态为：

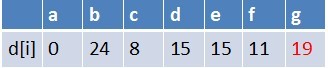
在最短路径表中，g的最短路径估值没有变小（松弛不成功），没有新结点入队，队列中元素为f，g

队首元素f点出队，对以f为起始点的所有边的终点依次进行松弛操作（此处有d，e，g三个点），此时路径表格状态为：

在最短路径表中，e，g的最短路径估值又变小，队列中无e点，e入队，队列中存在g这个点，g不用入队，此时队列中元素为g，e

队首元素g点出队，对以g为起始点的所有边的终点依次进行松弛操作（此处只有b点），此时路径表格状态为：

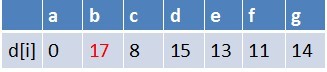
在最短路径表中，b的最短路径估值又变小，队列中无b点，b入队，此时队列中元素为e，b
队首元素e点出队，对以e为起始点的所有边的终点依次进行松弛操作（此处只有g这个点），此时路径表格状态为：

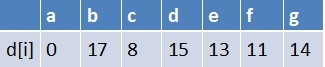
在最短路径表中，g的最短路径估值没变化（松弛不成功），此时队列中元素为b

队首元素b点出队，对以b为起始点的所有边的终点依次进行松弛操作（此处只有e这个点），此时路径表格状态为：

在最短路径表中，e的最短路径估值没变化（松弛不成功），此时队列为空了

最终a到g的最短路径为１４