五一培训 DAY1
DAY 1 2019.4.28
例题1
题解：
例题2
题解：
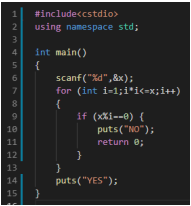
例题3
题解：
vis[ ]判断是否为素数，pri[ ]储存素数
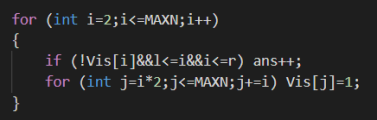
例题4
题解：
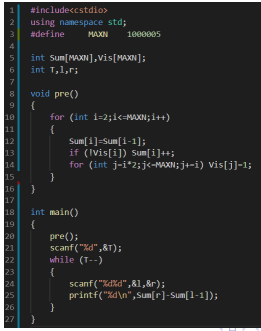
例题5
题解：
PS： i < 1<<n i<2^n
(1<<j）& i 如果2^j最后一位和 i 相同，返回1
例题6
判回文数是N√N，素数NlogN
枚举：
1.从起点开始向四个方向扩展
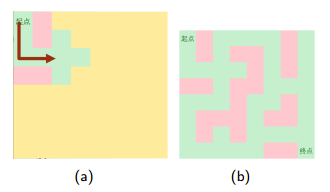
2.到一个点卡死，删除栈中的位置，回到前一步继续搜
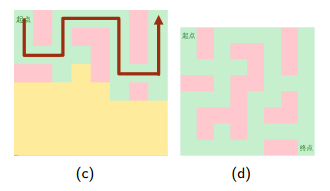
3.找到一种解
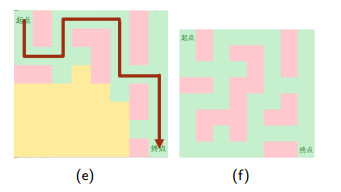
4.这也是一个解
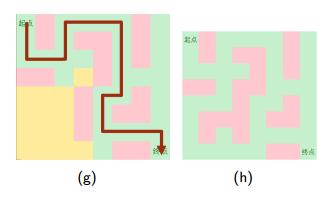
PS：DFS不会死循环，走完一个方向就会走其他方向
例题：
题解：
实际上就是寻找是否存在路径小于等于T
VIS[ ][ ]判断这个坐标是否走过
PS：
１．DFS使用一遍之后清空所影响数据
２．命名变量不要重名
每组数据开始之前ans要回归初始值
［代码］：
#include<cstdio>
#include<algorithm> #define N 15 using namespace std; int i,j,m,n,p,k,vis[N][N],tmp,T,ans=,tot; char c[N][N]; pair<int,int> Ans[N*N]; const int X[]={,,-,};
const int Y[]={-,,,}; int check(int x,int y) //是否合法
{
if (x<=||y<=||x>n||y>n) return ;
if (vis[x][y]) return ;
if (c[x][y]=='#') return ;
return ;
} void dfs(int x,int y)
{
if (c[x][y]=='E')
{
ans=min(ans,tot);
return;
}
vis[x][y]=;
Ans[++tot]=make_pair(x,y);
int i; //辅助变量，开在里面
for (i=;i<;++i)
if (check(x+X[i],y+Y[i]))
dfs(x+X[i],y+Y[i]);
--tot;
vis[x][y]=;
} void Main()
{
ans=(int)1e9;
scanf("%d%d",&n,&T);
for (i=;i<=n;++i) scanf("%s",c[i]+);
for (i=;i<=n;++i)
for (j=;j<=n;++j)
if (c[i][j]=='S') dfs(i,j);
printf(ans<=T?"YES\n":"NO\n");
} int main()
{
int T;
scanf("%d",&T);
for (;T--;) Main(); //用一个过程实现多组数据，模块化
}
１．沿四个方向扩展
２．起点出发，四周搜，可以走，加队列
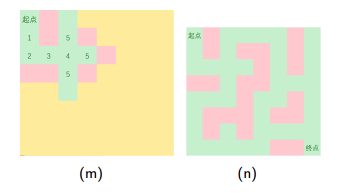
３．维护每个点距离起点的最短距离
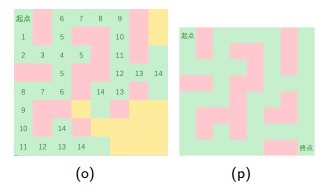
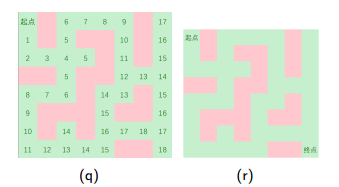
［代码］：
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<iostream>
#include<ctime>
#include<cmath>
#include<map>
#include<set>
#include<bitset>
#include<vector> #define ls (t<<1)
#define rs ((t<<1)|1) #define N 15
#define M 200005
#define K 17 #define pb push_back
#define fi first
#define se second
#define mk make_pair using namespace std; int i,j,n,m,Time; char c[N][N]; int vis[N][N]; pair<int,int> Q[N*N]; const int x[]={-,,,};
const int y[]={,,-,}; int check(int x,int y)
{
if (x<||y<||x>n||y>n) return ;
if (c[x][y]=='#') return ;
if (vis[x][y]!=-) return ;
return ;
} int bfs(int sx,int sy)
{
int i,l,r;
memset(vis,-,sizeof(vis));
Q[r=]=mk(sx,sy); vis[sx][sy]=;
for (l=;l<=r;++l)
{
int ax=Q[l].fi,ay=Q[l].se;
if (c[ax][ay]=='E')
{
if (vis[ax][ay]<=Time) return ;
return ;
}
for (i=;i<;++i)
if (check(ax+x[i],ay+y[i]))
{
Q[++r]=mk(ax+x[i],ay+y[i]);
vis[ax+x[i]][ay+y[i]]=vis[ax][ay]+;
}
}
return ;
} int main()
{
int T; scanf("%d",&T);
for (;T--;)
{
scanf("%d%d",&n,&Time);
for (i=;i<=n;++i) scanf("%s",c[i]+);
for (i=;i<=n;++i)
for (j=;j<=n;++j) if (c[i][j]=='S') {
if (bfs(i,j)) puts("YES"); else puts("NO");
}
}
}
DFS 先扩展，不行就回头
存储空间小
BFS 一般是求最短路径
全部走，所有路径集合，空间大
为所有可能的结果开数据
Pair 数组相当于一个结构体，int int两个元素，存横纵坐标
Vector
Vector可以用来存图存数据
可以自己定义类型
相当于开了N个int数组，长度可以很长
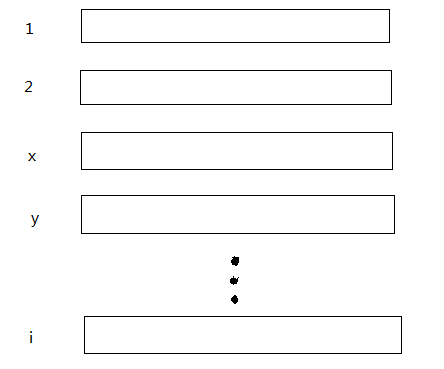
其实相当于开了一个二维数组
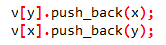
相当于在数组第y行最后加入一个x
在数组第x行最后加入一个y
每一行数组表示该点可以到达的点（也就是这两个点之间联通）
弹出
[代码]：
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<iostream>
#include<ctime>
#include<cmath>
#include<map>
#include<set>
#include<bitset>
#include<vector> #define ls (t<<1)
#define rs ((t<<1)|1) #define N 100005
#define M 200005
#define K 17 #define pb push_back
#define fi first
#define se second
#define mk make_pair using namespace std; vector<int>v[N]; int i,j,m,n,p,k,vis[N],Q[N],ans; void bfs(int x)
{
int l,r;
Q[r=]=x;
vis[x]=;
for (l=;l<=r;++l)
{
int p=Q[l];
for (i=;i<(int)v[p].size();++i) //遍历所有出边
{
int k=v[p][i]; //vector类型其实相当于二维数组
if (vis[k]) continue;
vis[k]=;
Q[++r]=k;
}
}
} int main()
{
scanf("%d%d",&n,&m);
for (i=;i<=m;++i)
{
int x,y;
scanf("%d%d",&x,&y);
v[y].push_back(x);
v[x].push_back(y);
}
for (i=;i<=n;++i)
if (!vis[i])
{
bfs(i);
ans++;
} cout<<ans; }
PS：
k=奇数 => k^=1为k=k-1
k=偶数 => k^=1为k=k+1
[代码]：
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<iostream>
#include<ctime>
#include<cmath>
#include<map>
#include<set>
#include<bitset>
#include<vector> #define ls (t<<1)
#define rs ((t<<1)|1) #define N 1005
#define M 200005
#define K 17 #define pb push_back
#define fi first
#define se second
#define mk make_pair using namespace std; int i,j,m,n,p,k,r[]; int vis[N][N]; pair<int,int> Q[][N*N]; char c[N][N]; const int X[]={-,,,};
const int Y[]={,,-,}; int check(int x,int y)
{
if (x<=||y<=||x>n||y>m) return ;
if (vis[x][y]) return ;
return ;
} void bfs(int x,int y)
{
int i,l,now=;
Q[][r[]=]=make_pair(x,y);
memset(vis,-,sizeof(vis));
vis[x][y]=;
for (;;) //死循环
{
now^=;
if (!r[now]) return;
for (l=;l<=r[now];++l)
{
int ax=Q[now][r[now]].first,ay=Q[now][r[now]].second;
for (i=;i<;++i)
if (check(ax+X[i],ay+Y[i]))
{
int ck=c[ax+X[i]][ay+Y[i]]=='#';
if (!ck) //如果可以走，加入当前队列
{
vis[ax+X[i]][ay+Y[i]]=vis[ax][ay];
Q[now][++r[now]]=make_pair(ax+X[i],ay+Y[i]);
}
else // 否则加入暂时先不扩展的队列
{
vis[ax+X[i]][ay+Y[i]]=vis[ax][ay]+;
Q[now^][++r[now^]]=make_pair(ax+X[i],ay+Y[i]);
}
} // 维护两个不同的队列
}
}
} int main()
{
scanf("%d%d",&n,&m);
for (i=;i<=n;++i) scanf("%s",c[i]+);
for (i=;i<=n;++i)
for (j=;j<=m;++j)
if (c[i][j]=='S') bfs(i,j);
for (i=;i<=n;++i)
for (j=;j<=m;++j)
if (c[i][j]=='E') printf("%d\n",vis[i][j]);
}
能BFS就BFS，否则考虑DFS
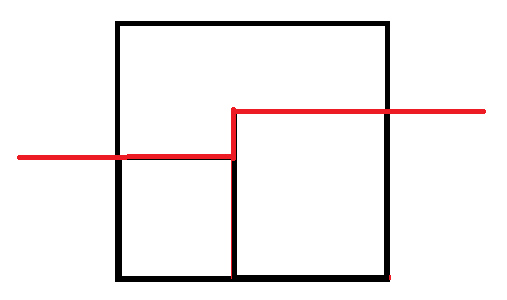
K表示有没有用过正方形
Id表示高度，不可以超边界
代码加了剪枝
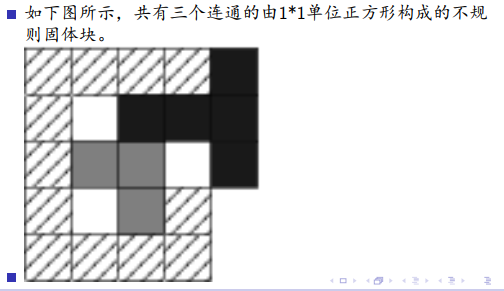
一个固体块，确定一个小块的位置，其余小块的位置就可以确定，整个固体块也就确定了
比如，（ a, b ） 第一块固体块的左上角方块坐标
（ c , d ） 第二块固体块的左上角方块坐标
（ e , f ） 第三块固体块的左上角方块坐标
然后根据相对位置推出其余小块的坐标
六维
比如，（ 0 , 0 ） 第一块固体块的左上角方块坐标
（ c , d ） 第二块固体块的左上角方块坐标
（ e , f ） 第三块固体块的左上角方块坐标
然后根据相对位置推出其余小块的坐标
移动的话要根据相对位置
状态数404，
一个四维状态
化简一下
ans=∑(Ai – Bi)*j+Bi*n- Ai
Ai – Bi越小越靠后
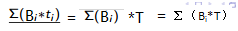
∑Bi（ti-T）=0
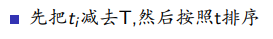
我们会得到一半正的一半负的
正：∑Bi，ti-T
负：∑Bi，ti-T
若|正|<|负|
那么正的就全取，负的有一部分为之抵消，至于未能抵消掉的，就直接不开此水龙头
[代码]：
#include<cstdio>
#include<algorithm>
#include<cstring> #define N 300005 using namespace std; int a[N],t[N],i,j,m,n,p,k,id[N],ID[N],sum[N],T; double ans; int cmp(int x,int y)
{
return sum[x]<sum[y];
} int main()
{
scanf("%d%d",&n,&T);
for (i=;i<=n;++i)
{
scanf("%d",&a[i]);
}
for (i=;i<=n;++i) scanf("%d",&t[i]);
for (i=;i<=n;++i)
{
if (t[i]==T) ans+=a[i];
else if (t[i]<T) id[++id[]]=i,sum[i]=T-t[i];
else ID[++ID[]]=i,sum[i]=t[i]-T;
}
sort(id+,id+id[]+,cmp);
sort(ID+,ID+ID[]+,cmp);
long long suma=,sumb=;
for (i=;i<=id[];++i)
suma+=1ll*sum[id[i]]*a[id[i]];
for (i=;i<=ID[];++i)
sumb+=1ll*sum[ID[i]]*a[ID[i]];
if (suma<sumb)
{
swap(suma,sumb);
for (i=;i<=n;++i) swap(ID[i],id[i]);
}
for (i=;i<=ID[];++i) ans+=a[ID[i]];
for (i=;i<=id[];++i)
if (1ll*sum[id[i]]*a[id[i]]>=sumb)
{
ans+=.*sumb/sum[id[i]];
break;
}
else
{
ans+=a[id[i]];
sumb-=1ll*sum[id[i]]*a[id[i]];
}
printf("%.10lf\n",ans);
}
示例：
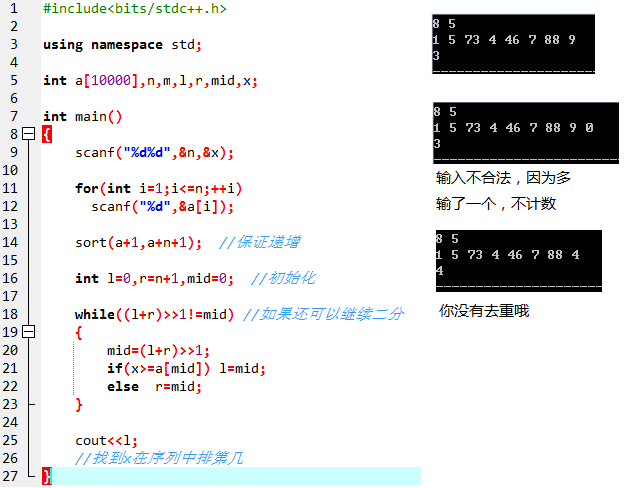
【代码】：
#include<bits/stdc++.h> using namespace std; int a[],n,m,l,r,mid,x; int main()
{
scanf("%d%d",&n,&x); for(int i=;i<=n;++i)
scanf("%d",&a[i]); sort(a+,a+n+); //保证递增 int l=,r=n+,mid=; //初始化 while((l+r)>>!=mid) //如果还可以继续二分
{
mid=(l+r)>>;
if(x>=a[mid]) l=mid;
else r=mid;
} cout<<l;
//找到x在序列中排第几
}
预处理相邻距离
距离最远的那次尽可能短
使用mid的跳跃是否合法
【代码】：
#iclude<bits/stdc++.h> #define N 300005 using namespace std; int i,j,m,n,p,k,a[N],x; int check(int x)
{
int i,cnt=;
for (i=;i<=n;++i) if (a[i]-a[i-]>x) return ; //跳不过去
for (i=;i<n;)
{
for (j=i;j<=n&&a[j]-a[i]<=x;++j);
++cnt;
i=j-;
}
if (cnt<=m) return ;
return ;
} int main()
{
scanf("%d%d",&n,&m);
for (i=;i<=n;++i) scanf("%d",&a[i]);
sort(a+,a+n+);
int l=,r=(int)1e9,mid=; //因为没有给定右端点
while ((l+r)>>!=mid)
{
mid=(l+r)>>;
if (check(mid)) r=mid;
else l=mid;
}
printf("%d\n",r);
}
P2678 跳石头
这也是个二分题，好像和刚才的不大一样
所以应该是：
#include<cstdio>
#include<algorithm>
#include<cstring> #define N 300005 using namespace std; int a[N],t[N],i,j,m,n,p,k,id[N],ID[N],sum[N],T; double ans; int cmp(int x,int y)
{
return sum[x]<sum[y];
} int main()
{
scanf("%d%d",&n,&T);
for (i=;i<=n;++i)
scanf("%d",&a[i]); for (i=;i<=n;++i) scanf("%d",&t[i]);
for (i=;i<=n;++i)
{
if (t[i]==T) ans+=a[i];
else if (t[i]<T) id[++id[]]=i,sum[i]=T-t[i];
else ID[++ID[]]=i,sum[i]=t[i]-T;
}
sort(id+,id+id[]+,cmp);
sort(ID+,ID+ID[]+,cmp);
long long suma=,sumb=;
for (i=;i<=id[];++i)
suma+=1ll*sum[id[i]]*a[id[i]];
for (i=;i<=ID[];++i)
sumb+=1ll*sum[ID[i]]*a[ID[i]];
if (suma<sumb)
{
swap(suma,sumb);
for (i=;i<=n;++i) swap(ID[i],id[i]);
}
for (i=;i<=ID[];++i) ans+=a[ID[i]];
for (i=;i<=id[];++i)
if (1ll*sum[id[i]]*a[id[i]]>=sumb)
{
ans+=.*sumb/sum[id[i]];
break;
}
else
{
ans+=a[id[i]];
sumb-=1ll*sum[id[i]]*a[id[i]];
}
printf("%.10lf\n",ans);
}
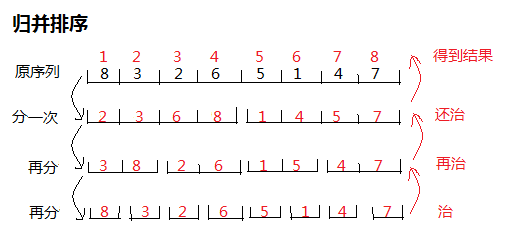
【代码】
#include<bits/stdc++.h> #define N 500005 using namespace std; int i,j,m,n,p,k,a[N],ty,x; long long b[N]; //表示前K个数的前缀和 double check(int x) //平均数
{
return .*(b[x-]+a[n])/x;
} int main()
{
scanf("%d",&m);
for (;m--;)
{
scanf("%d",&ty); //操作名称 if (ty==) //插入数的操作
{
scanf("%d",&x);
a[++n]=x;
b[n]=b[n-]+x;
} else
{
int l=,r=n;
while (r-l>) //保留一个尽量大的小三分区间，比如只有10个数
{
int len=(r-l+)/,mid1=l+len,mid2=mid1+len; //三分，每次缩小三分之一
if (check(mid1)<check(mid2)) r=mid2; //因为函数图像是倒着的
else l=mid1;
} //在区间内部枚举一下
double ans=;
for (i=l;i<=r;++i) ans=max(ans,a[n]-check(i));
printf("%.10lf\n",ans);
} }
}
五一培训 DAY1的更多相关文章
- 五一培训 清北学堂 DAY1
今天是冯哲老师的讲授~ 1.枚举 枚举也称作穷举,指的是从问题所有可能的解的集合中一一枚举各元素. 用题目中给定的检验条件判定哪些是无用的,哪些是有用的.能使命题成立的即为其解. 例一一棵苹果树上有n ...
- 纪中2018暑假培训day1提高b组改题记录
收到意见,认为每天的程序和随笔放在一起写的博客太长了,于是分开整理 day1 模拟赛,看了看提高a组t1的样例就不太想写,于是转而写b组 t1: Description 给定一个n个点m条边的有向图, ...
- 中山纪念中学培训DAY1
哇啊啊啊啊啊啊$……$ 并不像说环境怎么样. $Day1$模拟赛 稳重一点选了提高$B$ 然后$5min$后: $t1$装压$DP$最短路 $t2$裸地贪心 $t3……$哇$t3$怎么做啊啊啊啊. $ ...
- 五一培训 清北学堂 DAY4
今天上午是钟皓曦老师的讲授,下午是吴耀轩老师出的题给我们NOIP模拟考了一下下(悲催暴零) 今天的内容——数论 话说我们可能真的是交了冤枉钱了,和上次清明培训的时候的课件及内容一样(哭. 整除性 质数 ...
- 常州培训 day1 解题报告
第一题:(骗分容易,AC难.) 题目大意: 给出一个字符串,找出满足条件A的区间的个数.A:字符A,B,C的出现次数相同. 都出现0次也算,区间的长度可以是0(就是只有一个数).30% |S| ≤ 1 ...
- 五一培训 清北学堂 DAY2
今天还是冯哲老师的讲授~~ 今日内容:简单数据结构(没看出来简单qaq) 1.搜索二叉树 前置技能 一道入门题在初学OI的时候,总会遇到这么一道题.给出N次操作,每次加入一个数,或者询问当前所有数的最 ...
- 五一培训 清北学堂 DAY3
今天是钟皓曦老师的讲授~ 今天的内容:动态规划 1.动态规划 动态规划很难总结出一套规律 例子:斐波那契数列 0,1,1,2,3,5,8,…… F[0]=0 F[1]=1 F[[n]=f[n-1]+ ...
- 泉五培训Day1
T1 树学 题目 [问题描述] 给定一颗 n 个点的树,树边带权,试求一个排列 P,最大化下式 其中,calc(a, b)表示树上由a到b经过的最大边权. [输入格式] 第一行一个整数 n,表示点数下 ...
- 性能测试培训day1
测试本质: 1构造测试数据和期望结果 2执行 3验证 自动化测试: 写完代码,单元测试测代码逻辑,单元测试搞清楚代码逻辑就行了(白盒测试)先静态,运行前用工具扫描BUG例如(a==11写成a=11), ...
随机推荐
- jQuery (02) 重点知识点总结
jQuery 如果用户未登录,当加入购物车,会将商品相关信息存入 cookie 或者 session,这两个都是可以标识用户信息的东西 是一个 JavaScript 库,封装了常用的开发功能,和一些需 ...
- react_结合 redux - 高阶函数 - 高阶组件 - 前端、后台项目打包运行
Redux 独立的集中式状态管理 js 库 - 参见 My Git 不是 react 库,可以与 angular.vue 配合使用,通常和 react 用 yarn add redux import ...
- [LeetCode] To Lower Case 转为小写
Implement function ToLowerCase() that has a string parameter str, and returns the same string in low ...
- [LeetCode] N-ary Tree Postorder Traversal N叉树的后序遍历
Given an n-ary tree, return the postorder traversal of its nodes' values. For example, given a 3-ary ...
- [Educational Round 5][Codeforces 616F. Expensive Strings]
这题调得我心疲力竭...Educational Round 5就过一段时间再发了_(:з」∠)_ 先后找了三份AC代码对拍,结果有两份都会在某些数据上出点问题...这场的数据有点水啊_(:з」∠)_[ ...
- iOS—使用picker View
iOS—使用picker View 一.实现效果 说明:点击随机按钮,能够自动选取,下方数据自动刷新. 二.实现思路 1.picker view的有默认高度为162,不可修改. 2.显示数据,需要设置 ...
- go 并发编程(2)
协程 执行体是个抽象的概念,在操作系统层面有很多个概念与之对应,如操作系统自己掌管的进程(process),进程内的线程(thread),以及进程内的协程(coroutine,也叫轻量级线程).与传统 ...
- XenServer多网卡绑定
xenserver通过 XenCenter可以绑定网卡,支持Active-Active和Active-Standby的模式,但是通过Xencenter只能绑定两块网卡为一组.更多的比如3块一组.4块一 ...
- ACM练习中关于LCS的题目
You are planning to take some rest and to go out on vacation, but you really don’t know which cities ...
- Jmeter学习之--dubbo接口测试
背景:公司的h5和APP都需要调用许多非http的服务,需要对服务的性能和自动化测试 工具:IDEA ,maven,Jmeter 参考文档: https://testerhome.com/topics ...