Decision tree——决策树

基本流程

　　决策树是通过分次判断样本属性来进行划分样本类别的机器学习模型。每个树的结点选择一个最优属性来进行样本的分流，最终将样本类别划分出来。

　　决策树的关键就是分流时最优属性$a$的选择。使用所谓信息增益$Gain(D,a)$来判别不同属性的划分性能，即划分前样本类别的信息熵，减去划分后样本类别的平均信息熵，显然信息增益越大越好：

$\text{Ent}(D)=-\sum\limits_{k=1}^{|\mathcal{Y}|}p_k\log_{2}p_k$
$\displaystyle\text{Gain}(D,a)=\text{Ent}(D)-\sum\limits_{v=1}^{V}\frac{|D^v|}{|D|}\text{Ent}(D^v)$

　　其中$D$是划分前的数据集，$|\mathcal{Y}|$是样本的类别数，$p_k$是数据集中类别$k$的比例，$D^v$是划分后的某个数据集，$V$是数据集的分流数量。

　　又考虑到可能有的属性取值过多，直接将样本划分为多个只包含一个样本的集合，信息熵变为了0。如此似乎取得最大的信息增益，但实际上是过拟合了。因此，还要使用“增益率”来平衡，除了信息增益要大外，划分出的集合数要小。增益率定义如下：

$\text{Gain_ratio}(D,a)=\displaystyle \frac{\text{Gain(D,a)}}{\text{IV}(a)},$

$\displaystyle\text{IV}(a)=-\sum\limits_{v=1}^V\frac{|D^v|}{|D|}\log_{2}\frac{|D^v|}{|D|}$

　　另外，也不能一味地取增益率大的属性，因为大增益率偏好属性种类少的属性，也就会偏好连续属性（因为连续属性是取一个划分点来将样本划分为两部分，而离散属性则可能有多个属性种类）。因此通常会启发性地先选出信息增益大于平均值的属性，再从其中选择增益率最大的属性。

实验

　　训练数据集使用西瓜数据集：

　　实验没有使用python的机器学习包sklearn，分别测试了使用与不使用增益率来生成决策树。 首先自定义树结点的结构，分别是离散属性结点、连续属性结点与叶结点，如下：

 node(离散):
 {
     "divide_attr": ["纹理", , , ],        //0：属性名称（第几个属性） //1：属性序号  //2：0离散，1连续     //3：连续属性的划分点
     "if_leave": false,            //是否为叶结点
     "info_gain": 0.3805918973682686,    //信息增益
     "gain_ratio": 0.2630853587192754,    //信息率
     "divide":
     {
         "清晰":node,
         "稍糊":node,
         "模糊":node
     }//存各个样式的结点
 }
 node(连续):
 {
     "divide_attr": ["密度", , , 0.3815],
     "if_leave": false,
     "info_gain": 0.7642045065086203,
     "gain_ratio": 1.0,
     "divide":
     {
         "":node,            //小于等于划分点
         "":node            //大于划分点
     }//存各个样式的结点
 }
 node(叶结点):
 {
     "if_leave":true,
     "class":"是"            //判断类别
     "samples":[...]            //存生成决策树时划分到这个叶结点的样本
 }

　　结点使用字典存储。

　　将数据输入Excel中并在python中读入，然后使用处理好的数据生成决策树。以下是不使用增益率生成的决策树结构：

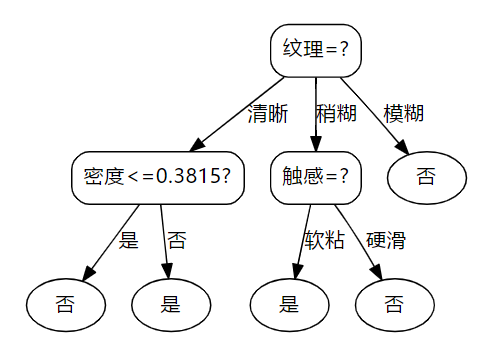
　　以下是使用增益率生成的决策树结构：

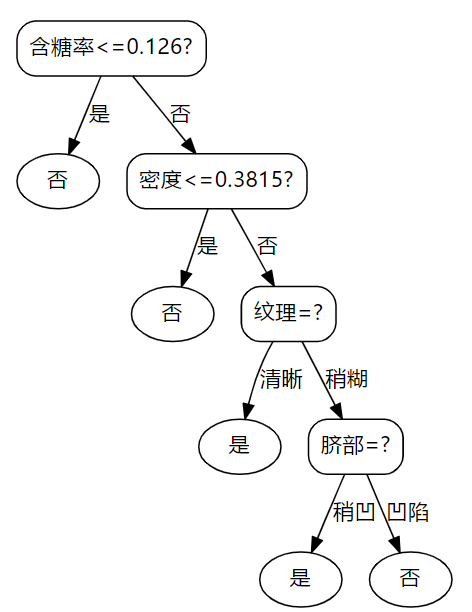
　　对比可以发现，当增益率参与决策树的生成时，连续属性会优先被使用。使用以上二者进行对训练集进行测试的正确率都是1.0。以下是处理数据、生成决策树、训练集验证、画出决策树结构的代码：

 #%%
 import matplotlib as plt
 import numpy as np
 import xlrd
 import sys

 table = xlrd.open_workbook('data.xlsx').sheets()[0]#读取Excel数据
 data = []
 for i in range(0,table.nrows):
     data.append(table.row_values(i))  

 attr_type = np.zeros([len(data[0])-2])#获取属性类型0离散，1连续
 for i in range(len(attr_type)):
     if type(data[1][i+1]) == str:
         attr_type[i] = 0
     else:
         attr_type[i]=1

 data = np.array(data)[:,1:] #转为数字矩阵 并去掉序号
 all_attr = data[0,:-1]  #存属性名称
 data = data[1:]#去掉表头   

 #%%
 def get_info_entropy(a):
     """
     传入array或list计算类别的信息熵
     """
     c = {}
     n = len(a)
     for i in a:
         if i not in c.keys():
             c[i] = 1
         else:
             c[i] += 1
     entropy = 0
     for i in c.keys():
         p = c[i]/n
         entropy += -p*np.log2(p)
     return entropy  

 def info_gain_and_ratio(D,s):
     """
     传入原数据集、按属性分类后的字典s
     """
     info_gain  = get_info_entropy(D[:,-1])
     class_entro = 0
     for i in s.keys():
         n = len(s[i])
         info_gain -= n/len(D)*get_info_entropy(s[i][:,-1])
         class_entro-=n/len(D)*np.log2(n/len(D))
     if class_entro == 0:
         return info_gain,info_gain
     return info_gain,info_gain/class_entro

 def attr_classfier(D,an,if_dic):
     """
     传入：数据集、分类属性序号、是否传出字典
     使用属性对D进行分类
     传出：
     1、离散：以属性值为key，以分类后的数据集为value的字典dictionary
     连续：key为0时<bound，为1时>bound
     2、连续属性的最优分界点float，离散的传出0
     3、类别信息增益
     4、增益率
     """
     dic = {}
     opt_bound = 0
     info_gain = 0
     gain_ratio = 0
     if attr_type[an] == 0:#离散属性获得分类数据集
         for i in D:
             if i[an] not in dic.keys():
                 dic[i[an]] = [i]
             else:
                 dic[i[an]].append(i)
         for i in dic.keys():
             dic[i] = np.array(dic[i])
         info_gain,gain_ratio = info_gain_and_ratio(D,dic)
     elif attr_type[an] == 1:#连续属性获得分类数据集
         attrs = D[:,an]
         attrs = np.sort(attrs.astype(float))
         for i in range(len(attrs)-1):
             bound = (attrs[i]+attrs[i+1])/2
             dic0 = {} #每次都初始化
             dic0[''] = []
             dic0[''] = []
             for j in D:
                 if float(j[an]) <= bound:
                     dic0[''].append(j)
                 else:
                     dic0[''].append(j)
             for j in dic0.keys():
                 dic0[j] = np.array(dic0[j])
             t,b = info_gain_and_ratio(D,dic0)
             if t>info_gain:
                 dic = dic0
                 opt_bound = bound
                 info_gain = t
                 gain_ratio = b
     if if_dic:
         return dic,opt_bound,info_gain,gain_ratio
     return opt_bound,info_gain,gain_ratio  

 def get_most_class(d):
     """
     获取数据集中占比最大的类别
     """
     c = {}
     for i in d[:,-1]:
         if i not in c.keys():
             c[i] = 1
         else:
             c[i] += 1
     m = ""
     for i in c.keys():
         if m == "":
             m = i
         elif c[i] > c[m]:
             m = i
     return m

 #%%
 def get_opt_attr(ave_info_gain,info_gains,gain_ratios,A,use_gain_ratios):
     """
     获取最优属性传入：
     1、平均信息增益
     2、所有属性的信息增益
     3、所有属性的信息率
     4、属性可用list
     5、是否使用信息率
     """
     opt_attr_index = 0
     #获取最优属性
     for i in range(len(A)):
         if A[i] == 1:
             if info_gains[i] > ave_info_gain:#在信息增益大于平均中取最大信息率
                 if use_gain_ratios:
                     if gain_ratios[i] > gain_ratios[opt_attr_index]:
                         opt_attr_index = i ################取到最优属性了
                 else:
                     if info_gains[i] > info_gains[opt_attr_index]:
                         opt_attr_index = i
     return opt_attr_index

 def create_node(D,A,use_gain_ratios):
     '''
     :传入数据集和属性集
     :D传入数据集的切片
     :A传入属性的使用矩阵，如[1,1,1,0,0,0,1],1表示可使用，0表示已使用
     :函数同一类别的先判断，之后属性取值全相同和划分属性放一起
     '''
     node = {}
     if len(set(D[:,-1])) == 1:#类别全相等，叶结点
         node["if_leave"]=True
         node["class"]=D[0,-1]
         node["samples"] = D.tolist()
         return node
     info_gains = np.zeros([len(A)]) #所有可用属性得出的信息增益
     ave_info_gain = 0#平均信息增益
     gain_ratios = np.zeros([len(A)])#所有可用属性得出的信息增益率
     opt_attr_index = 0#大于平均信息增益的属性中，增益率最大的属性索引
     attr_bound = np.zeros([len(A)])   #连续属性的属性界限
     active_attrN = 0 #可用属性数，用于求信息增益平均
     for i in range(len(A)):
         if A[i] == 1:
             attr_bound[i],info_gains[i],gain_ratios[i] =  attr_classfier(D,i,False)
             ave_info_gain += info_gains[i]
             active_attrN += 1
     """
     以下判断之一成立，即为叶结点，没有分下去的意义：
     # 1、所有属性增益率都太低
     # 2、所有属性是否分别在所有样本上取值都相同（同上，信息增益=0）
     # 3、可用属性为空
     """
     if ave_info_gain < 0.01 or active_attrN == 0:
         node["if_leave"] = True
         node["class"] = get_most_class(D[:,-1])#类别为数据集中最多的类
         node["samples"] = D.tolist()
         return node
     #获取最优属性
     opt_attr_index = get_opt_attr(opt_attr_index,info_gains,gain_ratios,A,use_gain_ratios)
     """
     以下由最优属性生成子结点
     """
     dic,bound,info_gain,gain_ratio= attr_classfier(D,opt_attr_index,True)
     if attr_type[opt_attr_index] == 0:#离散
         A[opt_attr_index] = 0
         node["divide_attr"] = [all_attr[opt_attr_index],opt_attr_index,0,0]
     elif attr_type[opt_attr_index] == 1:#连续
         node["divide_attr"] = [all_attr[opt_attr_index],opt_attr_index,1,bound]
     sons = {}
     for i in dic.keys():
         sons[i] = create_node(dic[i],A[:],use_gain_ratios)
     node["if_leave"] = False
     node["info_gain"] = info_gain
     node["gain_ratio"] = gain_ratio
     node["divide"] = sons
     return node

 """
 此处生成决策树，True使用增益率，False不用
 """
 root = create_node(data,np.ones([len(all_attr)]),False)

 #%%
 """
 以上训练好模型root，下面测试
 """
 def test_decision_tree(sample,tree):
     decision = ""
     while True:
         if tree["if_leave"] == True:
             decision = tree["class"]
             break
         if tree["divide_attr"][2] == 0:#离散
             attr = tree["divide_attr"][1]
             tree = tree["divide"][sample[attr]]
         elif tree["divide_attr"][2] == 1:#连续
             attr = tree["divide_attr"][1]
             b = tree["divide_attr"][3]
             if float(sample[attr]) <= b:
                 tree = tree["divide"][""]
             else:
                 tree = tree["divide"][""]
     return decision
 right = 0
 for i in data:
     a = test_decision_tree(i,root)
     if i[-1] == a:
         right +=1
 print("正确率：" + str(right/len(data)))
 #%%
 """
 Json导出树的结构
 """
 import json
 with open('decision tree.json','w',encoding='utf-8') as f:
     f.write(json.dumps(root,ensure_ascii = False))
 #%%
 """
 画出决策树结构
 """
 import pydotplus as pdp 

 def iterate_tree(tree,num):
     """
     迭代决策树，递归出结点间的箭头map
     """
     map_str = ""
     itenum = num
     if tree["if_leave"]:
         map_str = str(num)+'[label="' + tree["class"] + '"];' #类别
         map_str += str(num)+'[shape=ellipse];' #显示为椭圆
     else:
         if tree["divide_attr"][2] == 0:#离散属性
             map_str = str(num)+'[label="' + tree["divide_attr"][0] + '=?"];' #判别属性
             for i in tree["divide"].keys():
                 itenum+=1
                 map_str += str(num)+"->"+str(itenum)+'[label="'+ i +'"];' #添加边与边标签
                 son_map_str, itenum= iterate_tree(tree["divide"][i],itenum)
                 map_str+=son_map_str
         elif tree["divide_attr"][2] == 1:#连续属性
             map_str = str(num)+'[label="' + tree["divide_attr"][0] +"<="+ str(tree["divide_attr"][3]) + '?"];' #判别属性标签
             itenum+=1
             map_str += str(num)+"->"+str(itenum)+'[label="是"];' #添加边与边标签
             son_map_str, itenum= iterate_tree(tree["divide"][""],itenum)
             map_str+=son_map_str
             itenum+=1
             map_str += str(num)+"->"+str(itenum)+'[label="否"];' #添加边与边标签
             son_map_str, itenum= iterate_tree(tree["divide"][""],itenum)
             map_str+=son_map_str

     return map_str,itenum
 def get_decision_tree_map(tree):
     map_str = """
     digraph decision{
         node [shape=box, style="rounded", color="black", fontname="Microsoft YaHei"];
         edge [fontname="Microsoft YaHei"];
     """
     mm,n = iterate_tree(tree,0)
     return map_str + mm + "}"  

 decision_tree_map =  get_decision_tree_map(root)
 print(decision_tree_map)
 graph = pdp.graph_from_dot_data(decision_tree_map)
 graph.write_pdf("Decision tree.pdf")