5.10 省选模拟赛 tree 树形dp 逆元

LINK：tree

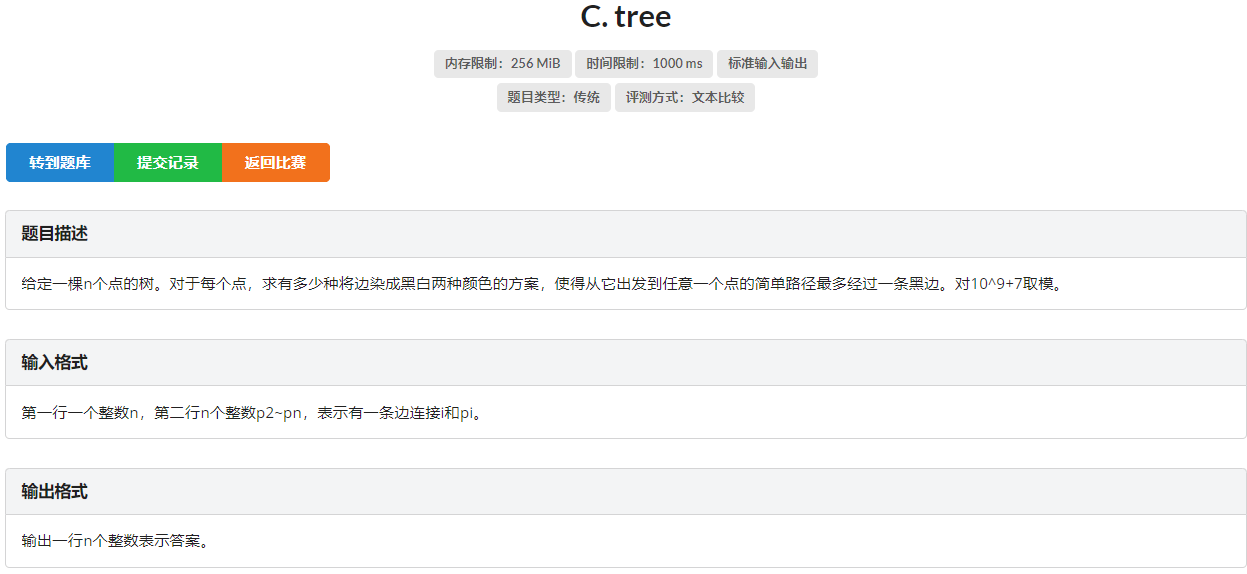
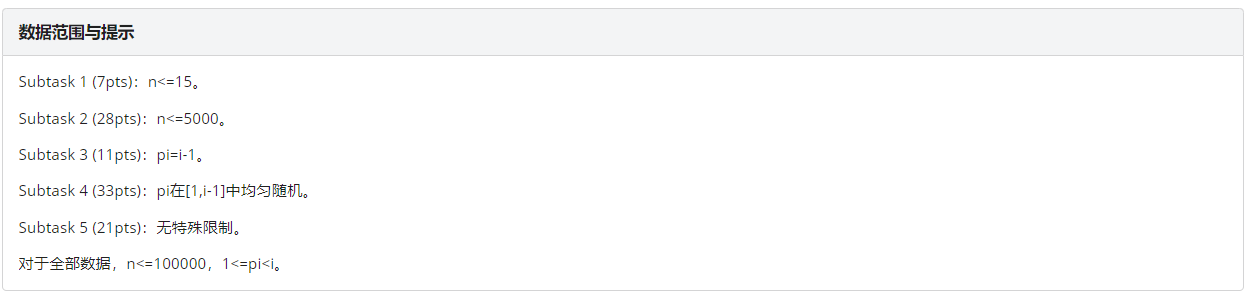
整场比赛看起来最不可做 确是最简单的题目。

感觉很难写 不过单独考虑某个点 容易想到树形dp的状态.

设f[x]表示以x为根的子树内有黑边的方案数。

白边方案只有一种所以不用记录。

转移 可能需要斟酌一下 我是列举了可能的所有情况 然后得到转移式子的。

\(f[x]=\Pi_{tn\in son_x}(f[tn]+2)-1\)

容易想到换根 容易发现可能不存在逆元 所以 需要乱搞一下.

(考场上没多想 看到树随机直接又接了一个暴力

就是没逆元再跑回去得到答案.(随机下挺快的不过我写挂了。

然后就是 处理前后缀积 也可以快速得到 可以利用vector 也可以直接记录除了某个点的前后缀积。

换根的时候 也要符合dp式子进行换根.我当时傻了开了vector 其实可以直接记录的。

const int MAXN=100010;
int n,len,top;
int f[MAXN],ans[MAXN],g[MAXN],id[MAXN],q[MAXN];
int lin[MAXN],ver[MAXN<<1],nex[MAXN<<1];
vector<int>w1[MAXN],w[MAXN];
inline void add(int x,int y)
{
	ver[++len]=y;nex[len]=lin[x];lin[x]=len;
	ver[++len]=x;nex[len]=lin[y];lin[y]=len;
}
inline void dfs(int x,int fa)
{
	int w2=1,ww=0;
	w[x].pb(1);w1[x].pb(1);
	go(x)if(tn!=fa)
	{
		dfs(tn,x);
		w2=(ll)w2*(1+f[tn]+1)%mod;
		w[x].pb(w2);
		w1[x].pb(w2);
		id[tn]=++ww;
	}
	w1[x].pb(1);w2=1;top=0;
	go(x)if(tn!=fa)q[++top]=tn;
	fep(top,1,i)
	{
		w2=(ll)w2*(2+f[q[i]])%mod;
		w1[x][i]=w2;
	}
	f[x]=(w2-1+mod)%mod;
}
inline void dp(int x,int fa,int v)
{
	if(x!=1){ans[x]=((ll)(f[x]+1)*v-1+mod)%mod;}
	go(x)if(tn!=fa)
		dp(tn,x,((ll)v*w[x][id[tn]-1]%mod*w1[x][id[tn]+1]+2-1)%mod);
}
int main()
{
	//freopen("1.in","r",stdin);
	get(n);
	rep(2,n,i)add(read(),i);
	dfs(1,0);ans[1]=f[1];
	dp(1,0,1);
	rep(1,n,i)put_((ans[i]+1)%mod);
	return 0;
}