7月15日考试 题解（链表+状压DP+思维题）

前言：蒟蒻太弱了，全打的暴力QAQ。

---------------------

T1 小Z的求和

题目大意：求$\sum\limits_{i=1}^n \sum\limits_{j=i}^n kth\max(a_i,a_{i+1},\cdots ,a_j)+kth\min(a_i,a_{i+1},\cdots ,a_j)$。其中$kthmax$指第$k$大，$kthmin$指第$k$小。

听hs-black说是链表维护，时间复杂度是$O(nk)$。然而并不会做……听了听学长的讲解。

对于这类问题，我们肯定是考虑每个元素对于答案的贡献的。（不然绝对会T飞

考虑$a[i]$从大到小添加，那么当有新加入的元素时，数轴为这样（假设$k=4$）：

红色为已经加入的元素，蓝色为新加入的元素，紫色是合法区间。

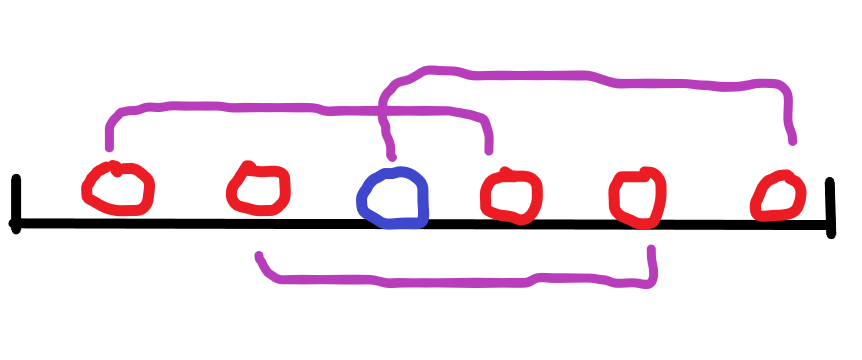
然后这个长度为$k$的区间从左到右移动，每次对于答案的贡献为$a[x]*(l-pre[l])*(nxt[r]-r)$。当所有贡献统计完后删除这个结点。

考虑到从大到小添加不易维护前驱和后缀，我们采用从小到大删除的方法，用链表维护。对于$kthmax$和$kthmin$只需相同方法求两遍就行了。时间复杂度$O(nk)$。

代码：

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int mod=;
int n,k,a[],pos[],ans;
int nxt[],pre[];
inline int read()
{
    int x=,f=;char ch=getchar();
    while(!isdigit(ch)){if (ch=='-') f=-;ch=getchar();}
    while(isdigit(ch)){x=x*+ch-'';ch=getchar();}
    return x*f;
}
bool cmp(int x,int y){return a[x]<a[y];}
inline void work()
{
    for (int i=;i<=n;i++) nxt[i]=i+,pre[i]=i-;
    for (int i=;i<=n;i++)
    {
        int l=pos[i],r=pos[i],cnt=;
        for (;cnt<k;cnt++)
        {
            if (pre[l]) l=pre[l];
            else break;
        }
        for (;cnt<k;cnt++)
        {
            if (nxt[r]<=n) r=nxt[r];
            else break;
        }
        if (cnt==k)
        {
            while(l<=pos[i])
            {
                if (r==n+) break;
                ans+=a[pos[i]]*(nxt[r]-r)*(l-pre[l])%mod;
                ans%=mod;
                l=nxt[l],r=nxt[r];
            }
        }
        pre[nxt[pos[i]]]=pre[pos[i]];
        nxt[pre[pos[i]]]=nxt[pos[i]];
    }
}
signed main()
{
    n=read(),k=read();
    for (int i=;i<=n;i++) a[i]=read(),pos[i]=i;
    sort(pos+,pos+n+,cmp);
    work();
    reverse(pos+,pos+n+);
    work();
    printf("%lld",ans%mod);
    return ;
}

T2 关押罪犯

题目大意：给定一张$n$个点，$m$条边的无向图。现在要求将这些点分成几组，每组边数不能超过$k$，且最小化分组数量。求分组最小值。

状压DP。然而我爆搜也能水不少分，$n\leq 16$。挂个$dfs$的代码吧。

代码：

#include<bits/stdc++.h>
using namespace std;
int n,m,k,a[][],ans=;
inline void dfs(int now,int cnt,int sum,int start)
{
    if (now==n){
        int tot=;
        for (int i=start;i<n;i++) if (a[i][now]) tot++;
        if (cnt+tot<=k) ans=min(ans,sum);
        else ans=min(ans,sum+);
        return;
    }
    int tot=;
    for (int i=start;i<now;i++) if (a[i][now]) tot++;
    dfs(now+,,sum+,now+);
    if (cnt+tot<=k) dfs(now+,cnt+tot,sum,start);
}
int main()
{
    cin>>n>>m>>k;
    for (int i=;i<=m;i++)
    {
        int x,y;cin>>x>>y;
        a[x][y]=a[y][x]=;
    }
    dfs(,,,);
    cout<<ans;
    return ;
}

T3 CF348D Turtles

引理：LGV定理。完全不会。听wyx大佬说可以不用定理，因为只有两条路径直接做就可以。

其实是一道思维题。

题意可以简化为从$(1,2)$到$(n-1,m)$和从$(2,1)$到$(n,m-1)$的路径不相交的方案数。然后，本题的精髓来了：

如果两条路径有相交，那么可以理解为这种情况是从$(1,2)$到$(n,m-1)$和从$(2,1)$到$(n-1,m)$的路径。这种情况是不合法的。所以我们只需要一步容斥一下，那么答案就是：

$calc(1,2,n-1,m)*calc(2,1,n,m-1)-calc(1,2,n,m-1)*clac(2,1,n-1,m)$

代码难度普及-，思维难度提高+。

代码：

//calc(1,2,n-1,m)*calc(2,1,n,m-1)-calc(2,1,n-1,m)*calc(1,2,n,m-1)
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int mod=1e9+;
long long n,m,f[][];
char vis[][];
inline int calc(int a,int b,int c,int d)
{
    memset(f,,sizeof(f));
    for (int i=a;i<=c;i++)
        for (int j=b;j<=d;j++)
        {
            if (vis[i][j]=='.'){
                if (i==a&&j==b) f[i][j]=;
                else f[i][j]=(f[i-][j]+f[i][j-])%mod;
            }
        }
    return f[c][d];
}
signed main()
{
    cin>>n>>m;
    for (int i=;i<=n;i++) scanf("%s",vis[i]+);
    int t1=calc(,,n-,m),t2=calc(,,n,m-);
    int t3=calc(,,n,m-),t4=calc(,,n-,m);
    cout<<((t1*t2%mod-t3*t4%mod)+mod)%mod;
    return ;
}