题解 SP687 【REPEATS - Repeats】

考虑可以枚举字符串上的两个点，求出两个点所对应后缀的\(LCP\)和所对应前缀的\(LCS\)，两点之间的距离为\(len\)，则这两个点对答案的贡献为：

\[ \frac{LCS+LCP+L-1}{L}
\]

取最大值即为答案，可以通过下图来理解这个式子：

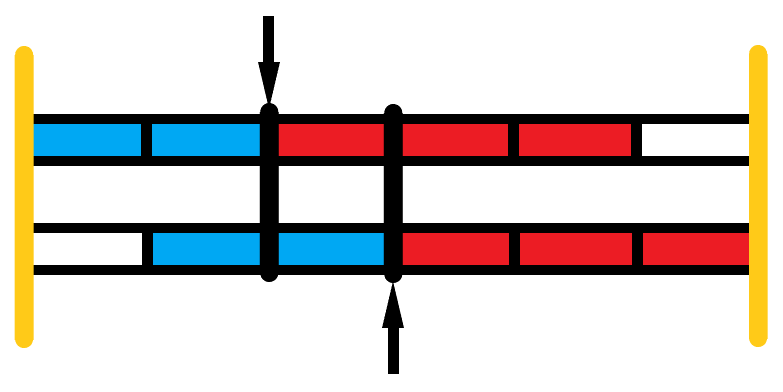
首先已经将字符串分为了若干个长度为\(len\)的块，箭头指向的位置为枚举的两个点，蓝色部分为\(LCS\)，红色部分为\(LCP\)，\(LCS+LCP+L-1\)即为黄色直线框起来的部分，不难发现，通过这样枚举点对，我们肯定能在其中一次枚举中找到重复次数最多的连续重复子串的重复次数。

枚举点对时可以枚举长度\(len\)，这样枚举复杂度就是\(O(n\ \log\ n)\)的了，求\(LCP\)和\(LCS\)用后缀数组实现即可。

\(code:\)

#include<bits/stdc++.h>
#define maxn 200010
using namespace std;
template<typename T> inline void read(T &x)
{
    x=0;char c=getchar();bool flag=false;
    while(!isdigit(c)){if(c=='-')flag=true;c=getchar();}
    while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
    if(flag)x=-x;
}
int T,n,ans;
struct node
{
    int n,m;
    int b[maxn],rk[maxn],sa[maxn],tp[maxn],ht[maxn];
    int lg[maxn],f[maxn][25];
    char s[maxn];
    void rsort()
    {
        for(int i=0;i<=m;++i) b[i]=0;
        for(int i=1;i<=n;++i) b[rk[i]]++;
        for(int i=1;i<=m;++i) b[i]+=b[i-1];
        for(int i=n;i;--i) sa[b[rk[tp[i]]]--]=tp[i];
    }
    void SA()
    {
        for(int i=1;i<=n;++i) rk[i]=s[i],tp[i]=i;
        rsort();
        for(int k=1;k<=n;k<<=1)
        {
            int num=0;
            for(int i=n-k+1;i<=n;++i) tp[++num]=i;
            for(int i=1;i<=n;++i)
                if(sa[i]>k)
                    tp[++num]=sa[i]-k;
            rsort(),memcpy(tp,rk,sizeof(rk)),rk[sa[1]]=num=1;
            for(int i=2;i<=n;++i)
                rk[sa[i]]=(tp[sa[i]]==tp[sa[i-1]]&&tp[sa[i]+k]==tp[sa[i-1]+k])?num:++num;
            if(num==n) break;
            m=num;
        }
        int k=0;
        for(int i=1;i<=n;++i) rk[sa[i]]=i;
        for(int i=1;i<=n;++i)
        {
            if(rk[i]==1) continue;
            if(k) k--;
            int j=sa[rk[i]-1];
            while(s[i+k]==s[j+k]) k++;
            ht[rk[i]]=k;
        }
    }
    void ST()
    {
        lg[0]=-1;
        for(int i=1;i<=n;++i) lg[i]=lg[i>>1]+1;
        for(int i=1;i<=n;++i) f[i][0]=ht[i];
        for(int j=1;j<=20;++j)
            for(int i=1;i+(1<<j)-1<=n;++i)
                f[i][j]=min(f[i][j-1],f[i+(1<<(j-1))][j-1]);
    }
    int query(int l,int r)
    {
        l=rk[l],r=rk[r];
        if(l>r) swap(l,r);
        l++;
        int len=lg[r-l+1];
        return min(f[l][len],f[r-(1<<len)+1][len]);
    }
    void init()
    {
        m=150,SA(),ST();
    }
}LCP,LCS;
int main()
{
    read(T);
    while(T--)
    {
        read(n),LCP.n=LCS.n=n,ans=0;
        for(int i=1;i<=n;++i) cin>>LCP.s[i],LCS.s[n-i+1]=LCP.s[i];
        LCP.init(),LCS.init();
        for(int len=1;len<=n;++len)
            for(int i=1;i+len<=n;i+=len)
                ans=max(ans,(LCP.query(i,i+len)+LCS.query(n-i+1,n-i-len+1)+len-1)/len);
        printf("%d\n",ans);
    }
    return 0;
}