Codeforces Round #671 (Div. 2) B. Stairs (递推)

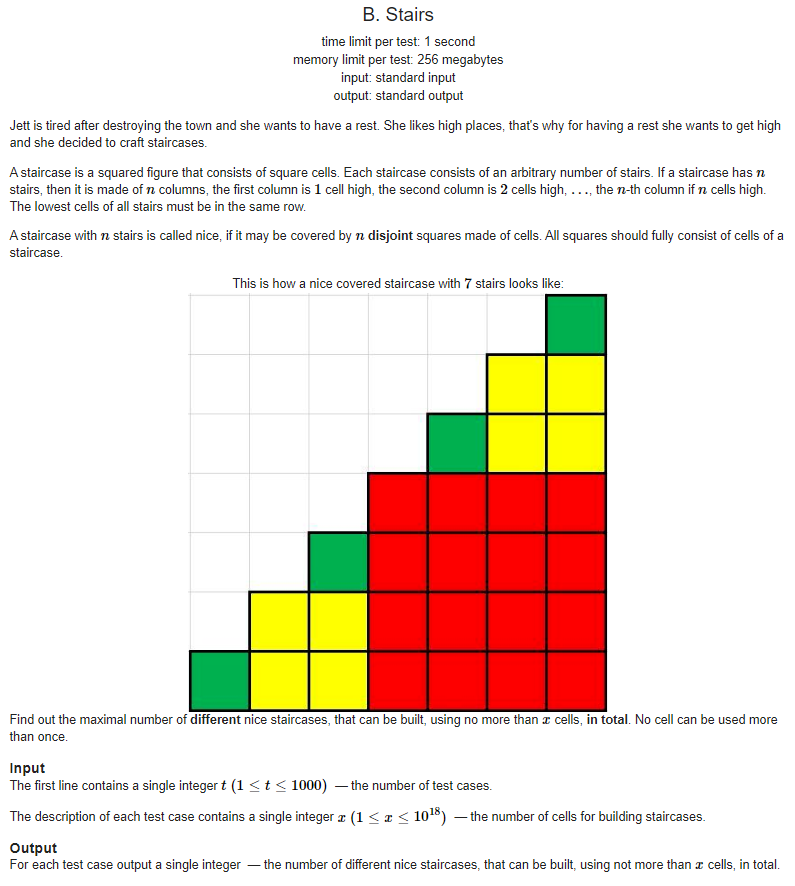
• 题意:一个台阶由一些单元格组成,如果一个高度为\(n\)的台阶中有\(n\)个不相邻的正方形(如图中的样例),就称这个台阶是"好台阶",现给你\(x\)个单元格,问最多能组成多少个"好台阶"?

• 题解:题目数据范围最多给了\(10^{18}\),而样例中的\(10^{18}\)最多有\(30\)个好台阶,而前几个"好台阶"的个数我们可以手算出来发现递推规律,\(f[i]=f[i-1]*2+(2^{i-1})^2\),所以我们预处理出来前\(30\)个好台阶,然后再去模拟一下就可以了.

• 代码:

  int t;
  ll n;
  ll pre[N];
  
  int main() {
      ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
  	cin>>t;
  	ll two=1;
  	for(int i=1;i<=30;++i){
  		pre[i]=pre[i-1]*2+two*two;
  		two*=2;
  	}
  	while(t--){
  		cin>>n;
  		int cnt=0;
  		for(int i=1;i<=30;++i){
  			n-=pre[i];
  			if(n>=0) cnt++;
  			else break;
  		}
  		cout<<cnt<<endl;
  	}
  
      return 0;
  }