【小白学PyTorch】12 SENet详解及PyTorch实现
文章来自微信公众号【机器学习炼丹术】。我是炼丹兄,有什么问题都可以来找我交流,近期建立了微信交流群,也在朋友圈抽奖赠书十多本了。我的微信是cyx645016617,欢迎各位朋友。
参考目录:
@
上一节课讲解了MobileNet的一个DSC深度可分离卷积的概念,希望大家可以在实际的任务中使用这种方法,现在再来介绍EfficientNet的另外一个基础知识—,Squeeze-and-Excitation Networks压缩-激活网络
1 网络结构
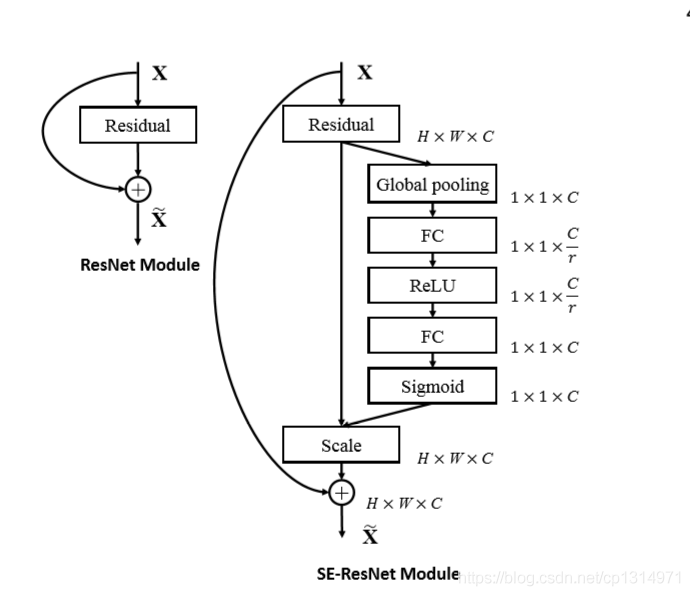
可以看出来,左边的图是一个典型的Resnet的结构,Resnet这个残差结构特征图求和而不是通道拼接,这一点可以注意一下
这个SENet结构式融合在残差网络上的,我来分析一下上图右边的结构:
- 输出特征图假设shape是\(W \times H \times C\)的;
- 一般的Resnet就是这个特征图经过残差网络的基本组块,得到了输出特征图,然后输入特征图和输入特征图通过残差结构连在一起(通过加和的方式连在一起);
- SE模块就是输出特征图先经过一个全局池化层,shape从\(W \times H \times C\)变成了\(1 \times 1 \times C\),这个就变成了一个全连接层的输入啦
压缩Squeeze:先放到第一个全连接层里面,输入\(C\)个元素,输出\(\frac{C}{r}\),r是一个事先设置的参数;
激活Excitation:在接上一个全连接层,输入是\(\frac{C}{r}\)个神经元,输出是\(C\)个元素,实现激活的过程;
- 现在我们有了一个\(C\)个元素的经过了两层全连接层的输出,这个C个元素,刚好表示的是原来输出特征图\(W \times H \times C\)中C个通道的一个权重值,所以我们让C个通道上的像素值分别乘上全连接的C个输出,这个步骤在图中称为Scale。而这个调整过特征图每一个通道权重的特征图是SE-Resnet的输出特征图,之后再考虑残差接连的步骤。
在原文论文中还有另外一个结构图,供大家参考:
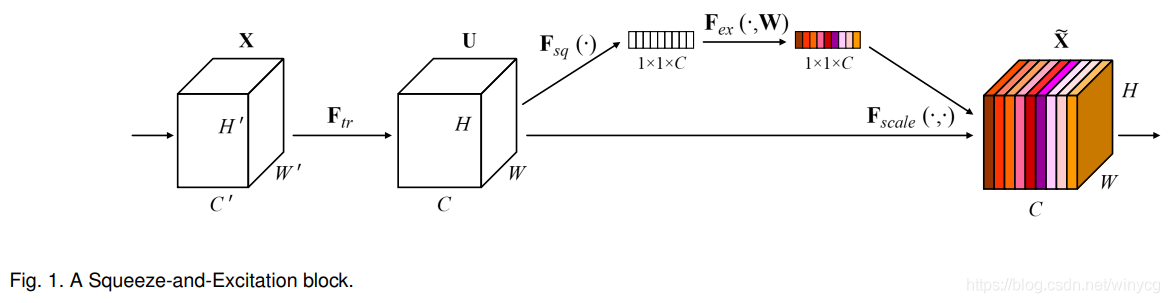
2 参数量分析
每一个卷积层都增加了额外的两个全连接层,不够好在全连接层的参数非常小,所以直观来看应该整体不会增加很多的计算量。 Resnet50的参数量为25M的大小,增加了SE模块,增加了2.5M的参数量,所以大概增加了10%左右,而且这2.5M的参数主要集中在final stage的se模块,因为在最后一个卷积模块中,特征图拥有最大的通道数,所以这个final stage的参数量占据了增加的2.5M参数的96%。
这里放一个几个网络结构的对比:
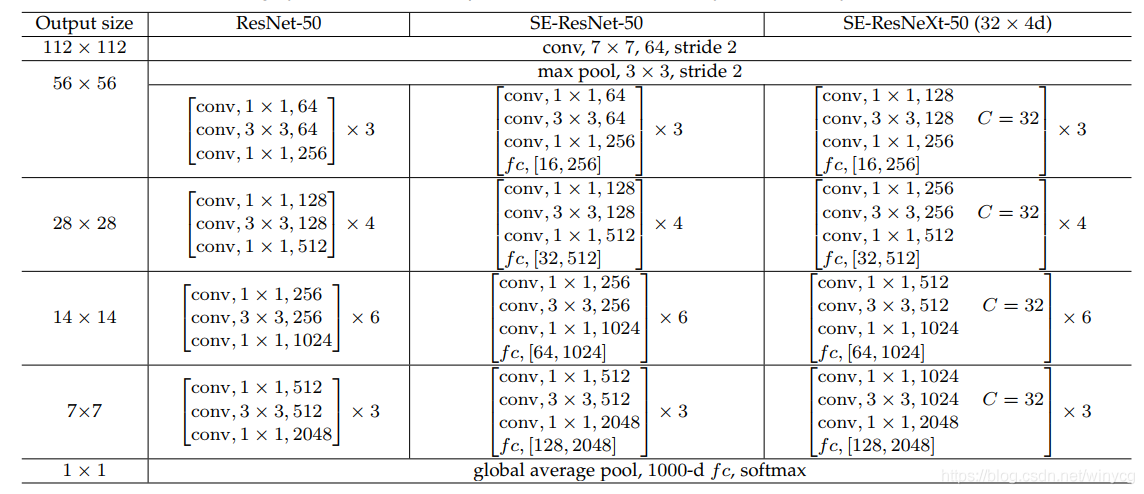
3 PyTorch实现与解析
先上完整版的代码,大家可以复制本地IDE跑一跑,如果代码有什么问题可以联系我:
import torch
import torch.nn as nn
import torch.nn.functional as F
class PreActBlock(nn.Module):
def __init__(self, in_planes, planes, stride=1):
super(PreActBlock, self).__init__()
self.bn1 = nn.BatchNorm2d(in_planes)
self.conv1 = nn.Conv2d(in_planes, planes, kernel_size=3, stride=stride, padding=1, bias=False)
self.bn2 = nn.BatchNorm2d(planes)
self.conv2 = nn.Conv2d(planes, planes, kernel_size=3, stride=1, padding=1, bias=False)
if stride != 1 or in_planes != planes:
self.shortcut = nn.Sequential(
nn.Conv2d(in_planes, planes, kernel_size=1, stride=stride, bias=False)
)
# SE layers
self.fc1 = nn.Conv2d(planes, planes//16, kernel_size=1)
self.fc2 = nn.Conv2d(planes//16, planes, kernel_size=1)
def forward(self, x):
out = F.relu(self.bn1(x))
shortcut = self.shortcut(out) if hasattr(self, 'shortcut') else x
out = self.conv1(out)
out = self.conv2(F.relu(self.bn2(out)))
# Squeeze
w = F.avg_pool2d(out, out.size(2))
w = F.relu(self.fc1(w))
w = F.sigmoid(self.fc2(w))
# Excitation
out = out * w
out += shortcut
return out
class SENet(nn.Module):
def __init__(self, block, num_blocks, num_classes=10):
super(SENet, self).__init__()
self.in_planes = 64
self.conv1 = nn.Conv2d(3, 64, kernel_size=3, stride=1, padding=1, bias=False)
self.bn1 = nn.BatchNorm2d(64)
self.layer1 = self._make_layer(block, 64, num_blocks[0], stride=1)
self.layer2 = self._make_layer(block, 128, num_blocks[1], stride=2)
self.layer3 = self._make_layer(block, 256, num_blocks[2], stride=2)
self.layer4 = self._make_layer(block, 512, num_blocks[3], stride=2)
self.linear = nn.Linear(512, num_classes)
def _make_layer(self, block, planes, num_blocks, stride):
strides = [stride] + [1]*(num_blocks-1)
layers = []
for stride in strides:
layers.append(block(self.in_planes, planes, stride))
self.in_planes = planes
return nn.Sequential(*layers)
def forward(self, x):
out = F.relu(self.bn1(self.conv1(x)))
out = self.layer1(out)
out = self.layer2(out)
out = self.layer3(out)
out = self.layer4(out)
out = F.avg_pool2d(out, 4)
out = out.view(out.size(0), -1)
out = self.linear(out)
return out
def SENet18():
return SENet(PreActBlock, [2,2,2,2])
net = SENet18()
y = net(torch.randn(1,3,32,32))
print(y.size())
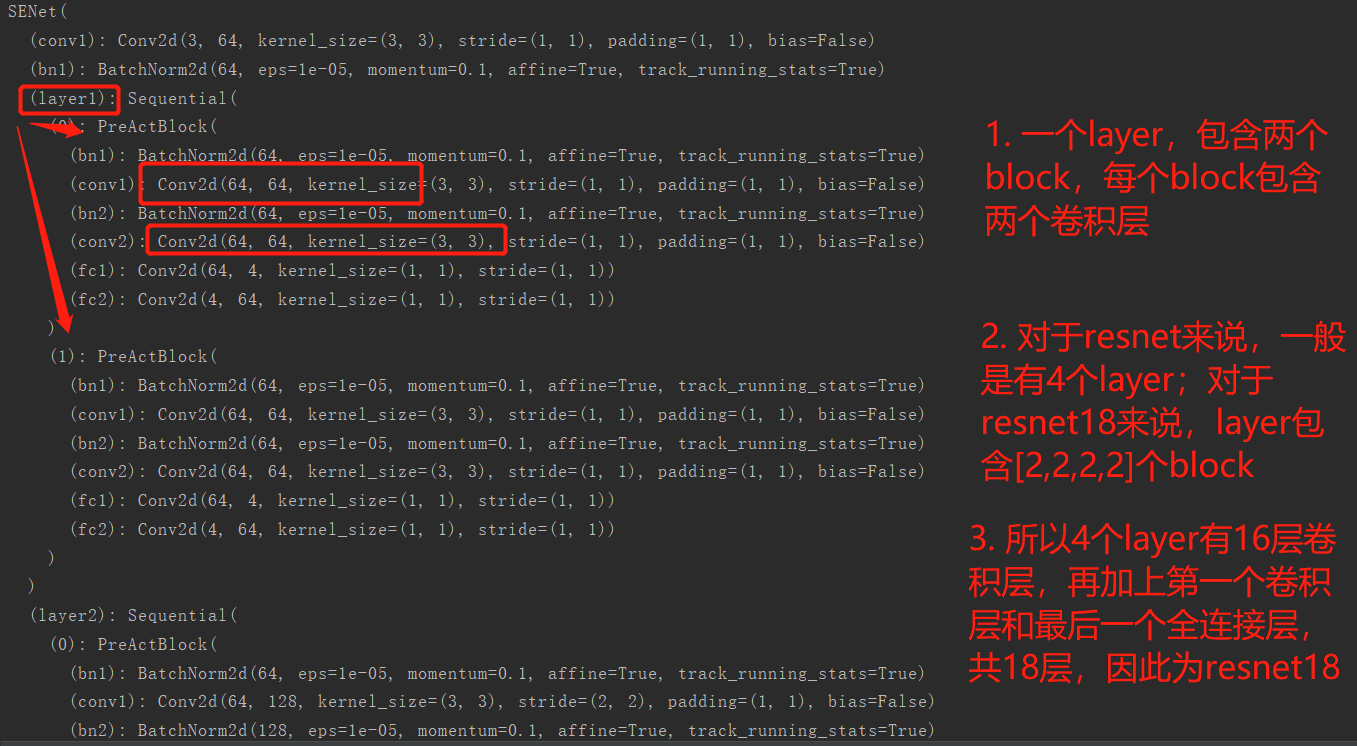
print(net)
输出和注解我都整理了一下:
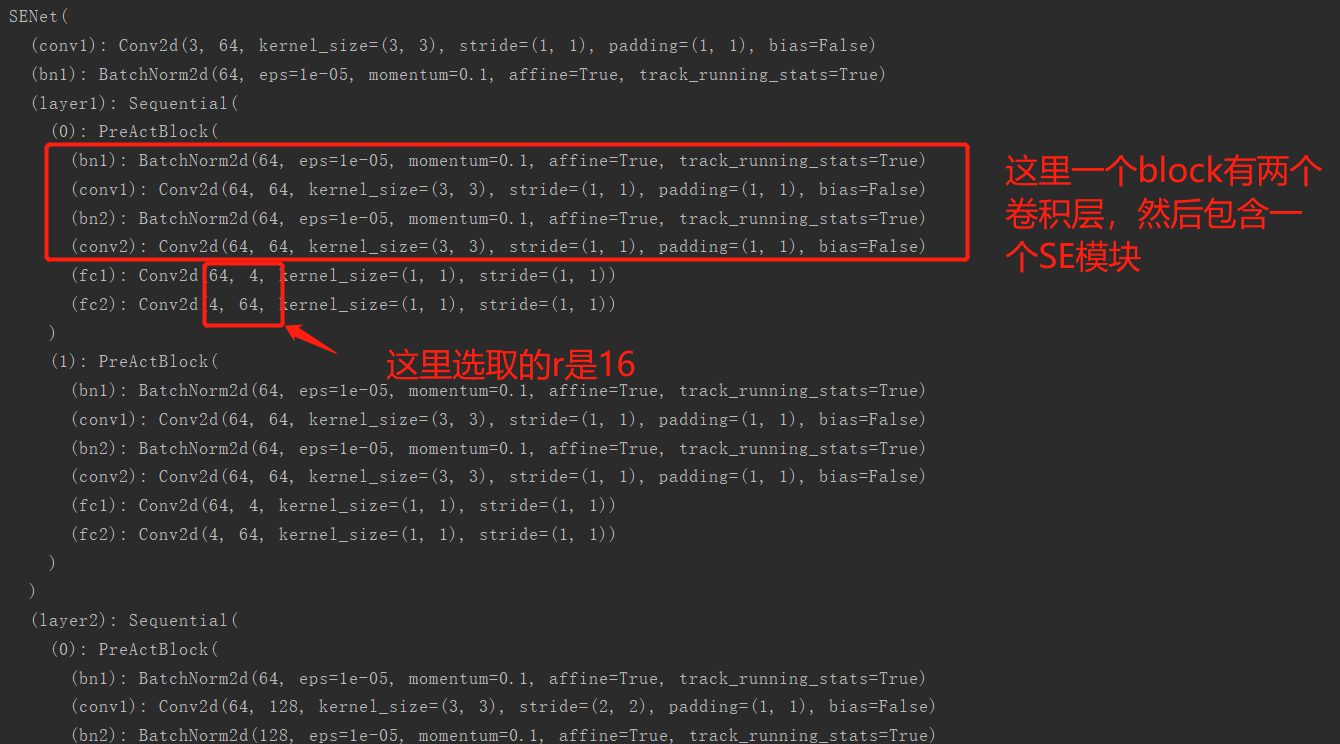
【小白学PyTorch】12 SENet详解及PyTorch实现的更多相关文章
- 【小白学PyTorch】11 MobileNet详解及PyTorch实现
文章来自微信公众号[机器学习炼丹术].我是炼丹兄,欢迎加我微信好友交流学习:cyx645016617. @ 目录 1 背景 2 深度可分离卷积 2.2 一般卷积计算量 2.2 深度可分离卷积计算量 2 ...
- html5--1.12表格详解
html5--1.12表格详解 一.总结 一句话总结: 二.详解 1.表格构成三个基本要素 table:表格的范围,外框:用来定义表格,表格的其他元素包含在table标签里面: tr: 表格的行: t ...
- Pytorch autograd,backward详解
平常都是无脑使用backward,每次看到别人的代码里使用诸如autograd.grad这种方法的时候就有点抵触,今天花了点时间了解了一下原理,写下笔记以供以后参考.以下笔记基于Pytorch1.0 ...
- SENet详解及Keras复现代码
转: SENet详解及Keras复现代码 论文地址:https://arxiv.org/pdf/1709.01507.pdf 代码地址:https://github.com/hujie-frank/S ...
- 【小白学PyTorch】13 EfficientNet详解及PyTorch实现
参考目录: 目录 1 EfficientNet 1.1 概述 1.2 把扩展问题用数学来描述 1.3 实验内容 1.4 compound scaling method 1.5 EfficientNet ...
- 【小白学PyTorch】10 pytorch常见运算详解
参考目录: 目录 1 矩阵与标量 2 哈达玛积 3 矩阵乘法 4 幂与开方 5 对数运算 6 近似值运算 7 剪裁运算 这一课主要是讲解PyTorch中的一些运算,加减乘除这些,当然还有矩阵的乘法这些 ...
- Pytorch数据读取详解
原文:http://studyai.com/article/11efc2bf#%E9%87%87%E6%A0%B7%E5%99%A8%20Sampler%20&%20BatchSampler ...
- javaweb基础(12)_session详解
一.Session简单介绍 在WEB开发中,服务器可以为每个用户浏览器创建一个会话对象(session对象),注意:一个浏览器独占一个session对象(默认情况下).因此,在需要保存用户数据时,服务 ...
- 【Linux】一步一步学Linux——Linux系统目录详解(09)
目录 00. 目录 01. 文件系统介绍 02. 常用目录介绍 03. /etc目录文件 04. /dev目录文件 05. /usr目录文件 06. /var目录文件 07. /proc 08. 比较 ...
随机推荐
- 序列化流(ObjectOutputStream、ObjectInputStream)
1.序列化流(ObjectOutputStream) package demo10.objstream; /* java.io.ObjectOutputStream extends OutputStr ...
- src rpm 下载地址
drbd: http://mirror.rackspace.com/elrepo/elrepo/el7/SRPMS/ rabbitmq: https://dl.bintray.com/rabbitmq ...
- Spring Security拦截器加载流程分析--练气中期
写在前面 上回我们讲了spring security整合spring springmvc的流程,并且知道了spring security是通过过滤器链来进行认证授权操作的.今天我们来分析一下sprin ...
- 面试28k职位,老乡面试官从HashCode到HashMap给我讲了一下午!「回家赶忙整理出1.6万字的面试材料」
作者:小傅哥 博客:https://bugstack.cn 目录 一.前言 二.HashCode为什么使用31作为乘数 1. 固定乘积31在这用到了 2. 来自stackoverflow的回答 3. ...
- Spring编程式注解使用不当导致其他事务无法正常提交
1.事故背景 原本在使用的是注解式事务,后面因为需要在事务中增加异步推送机制,所以需要将推送机制放到事务之外,修改后发现系统经常出现事务长时间无法提交导致回滚. 2.排查流程 (1)一开始重启应用是能 ...
- node_第三方包下载文件package.jon详解
配置原因第三方包的体积过大,不方便团队成员之间共享项目源代码共享时剔除node_modules 快速创建 package.json(只能在英文的目录下成功运行) npm init -y npm i 一 ...
- python练习 数字不同数之和+人名最多数统计
数字不同数之和 描述 获得用户输入的一个整数N,输出N中所出现不同数字的和. ...
- 基于laravel的有偿开源流程引擎
系统主要文档已经编写完成,具体请前往查看[系统文档](https://www.kancloud.cn/lijianlin/jishullin_workflow_engine/1894424 " ...
- 【Android】Android开发启动app弹出一张广告图片,Dialog可以查看大图,查看某个图片功能
作者:程序员小冰,GitHub主页:https://github.com/QQ986945193 新浪微博:http://weibo.com/mcxiaobing 首先给大家看一下我们今天这个最终实现 ...
- Unity 内嵌网页
uniwebview 官网 http://uniwebview.onevcat.com/reference/class_uni_web_view.html http://uniwebview.onev ...
