java性能问题排查提效脚本工具

在性能测试过程中，往往会出现各种各样的性能瓶颈。其中java常见瓶颈故障模型有cpu资源瓶颈；文件IO瓶颈；网络IO瓶颈；内存资源瓶颈；资源消耗不高程序本身执行慢等场景模型。

如何快速定位分析这些类型瓶颈？工欲善其事必先利其器。

 

本文主要讲述针对cpu高耗和网络IO瓶颈两个场景，使用排查提效脚本工具快速定位分析性能瓶颈

场景一：当服务器CPU高耗原因分析，如何快速定位到占用cpu高的用户线程

场景二：怀疑网络连接问题，如何快速分析网络TCP状态

 

原始做法：

场景一：

1. top命令找出消耗CPU高的Java进程及其线程id：

1. 开启线程显示模式（top -H，或是打开top后按H）
2. 按CPU使用率排序（top缺省是按CPU使用降序，已经合要求；打开top后按P可以显式指定按CPU使用降序）
3. 记下Java进程id及其CPU高的线程id

1. 查看消耗CPU高的线程栈：

1. 用进程id作为参数，jstack出有问题的Java进程
2. 把上述记录的10进制线程id手动转换成十六进制线程id（可以用printf %x 1234）
3. 在jstack输出中查找十六进制的线程id（可以用vim的查找功能/0x1234，或是grep 0x1234 -A 20）

1. 查看对应的线程栈，分析问题

排查问题时，会要多次上面的操作以分析确定问题，这个过程太繁琐太慢了。

场景二：

1.先用netstat命令分析网络TCP连接各个状态数。

2.然后tcpdump分析

排查问题时，命令复杂输入耗时，有时记不住，还得临时百度

 

推荐玩法：

打包下载整个提效工具脚本

wget --no-check-certificate https://github.com/oldratlee/useful-scripts/archive/release.zip

解压目录

unzip release.zip

文件中包含的常用脚本

推荐脚本用法：

场景一：

show-busy-java-threads脚本，用于快速排查Java的CPU性能问题(top us值过高)，自动查出运行的Java进程中消耗CPU多的线程，并打印出其线程栈，从而确定导致性能问题的方法调用。

show-busy-java-threads

# 从所有运行的Java进程中找出最消耗CPU的线程（缺省5个），打印出其线程栈

# 缺省会自动从所有的Java进程中找出最消耗CPU的线程，这样用更方便# 当然你可以手动指定要分析的Java进程Id，以保证只会显示你关心的那个Java进程的信息

show-busy-java-threads -p <指定的Java进程Id>

show-busy-java-threads -c <要显示的线程栈数>

show-busy-java-threads <重复执行的间隔秒数> [<重复执行的次数>]

# 多次执行；这2个参数的使用方式类似vmstat命令

show-busy-java-threads -a <运行输出的记录到的文件># 记录到文件以方便回溯查看

show-busy-java-threads -S <存储jstack输出文件的目录># 指定jstack输出文件的存储目录，方便记录以后续分析

示例：

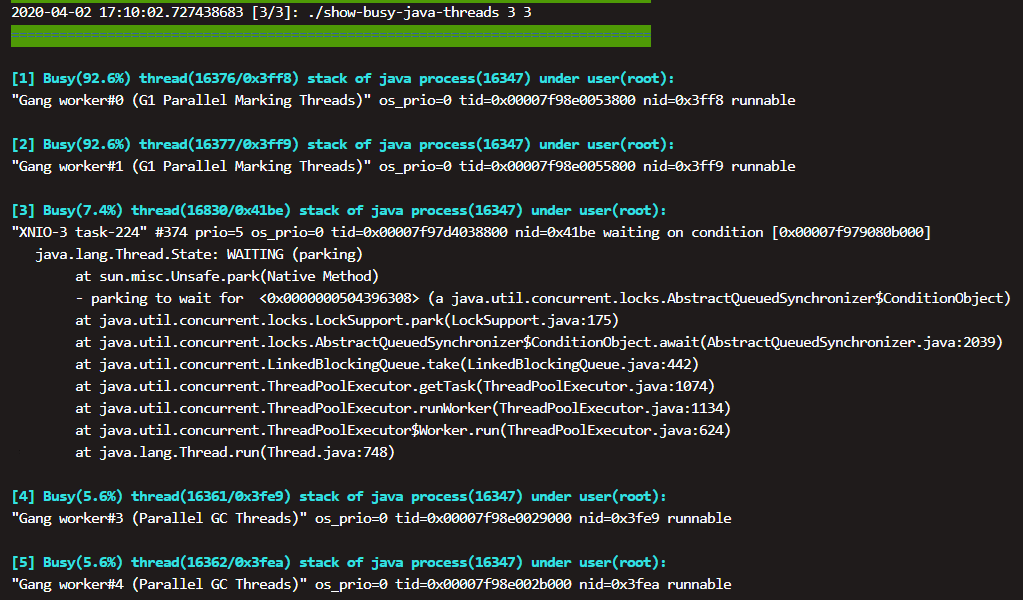
场景二：

tcp-connection-state-counter脚本，统计各个TCP连接状态的个数。

支持Linux、Mac、Windows（cygwin、MSSYS）。

像Nginx、Apache的机器上需要查看，TCP连接的个数，以判定

• 连接数、负荷
• 是否有攻击，查看SYN_RECV数（SYN攻击）
• TIME_WAIT数，太多会导致TCP: time wait bucket table overflow。

示例：

参考文档：

https://github.com/oldratlee/useful-scripts/blob/master/docs/java.md#-show-busy-java-threads