[BZOJ3684][拉格朗日反演+多项式求幂]大朋友和多叉树

题面

Description

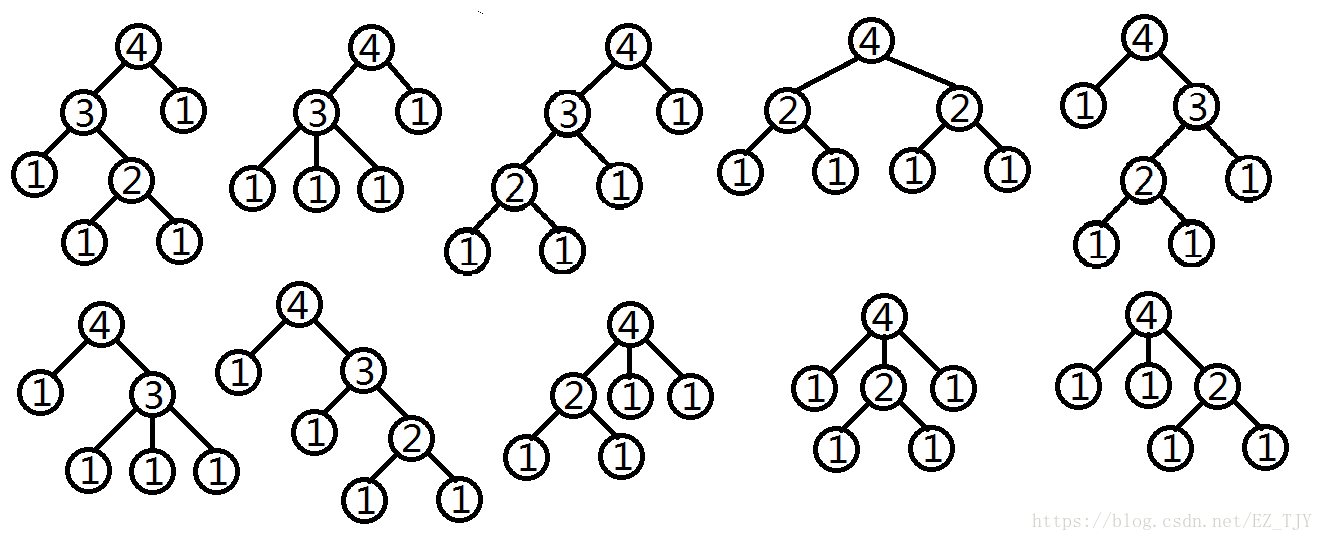
我们的大朋友很喜欢计算机科学，而且尤其喜欢多叉树。对于一棵带有正整数点权的有根多叉树，如果它满足这样的性质，我们的大朋友就会将其称作神犇的：点权为\(1\)的结点是叶子结点；对于任一点权大于\(1\)的结点\(u\)，\(u\)的孩子数目\(deg_u\)属于集合\(D\)，且\(u\)的点权等于这些孩子结点的点权之和。

给出一个整数\(s\)，你能求出根节点权值为\(s\)的神犇多叉树的个数吗？请参照样例以更好的理解什么样的两棵多叉树会被视为不同的。

我们只需要知道答案关于\(950009857\)（\(453\times2^{21}+1\)，一个质数）取模后的值。

Input

第一行有\(2\)个整数\(s,m\)。

第二行有\(m\)个互异的整数，\(d_1,d_2,\ldots,d_m\)，为集合\(D\)中的元素。

Output

输出一行仅一个整数，表示答案模\(950009857\)的值。

Sample Input

4 2

2 3

Sample Output

10

HINT

\(1\le m\le s\le10^5,2\le d_i\le s\)，有\(3\)组小数据和\(3\)组大数据。

分析

首先，我们设\(v_i\)为集合\(D\)中是否有\(i\)这个元素，有则为\(1\)，无则为\(0\)：$$v_i=\sum_{k=1}^{m}[d_k=i]$$

我们令\(V(x)\)为\(v_i\)的生成函数：$$V(x)=\sum_{k=0}^\infty v_i x^k$$

我们再设\(f_i\)为根节点权值为\(i\)的神犇多叉树的数量。

首先，显然有\(f_0=0\)；而当\(i=1\)即叶子节点时，有\(f_1=1\)。

而在\(i>1\)时，我们枚举根节点的儿子节点数量，在枚举各个叶子节点的权值，根据乘法原理得到递归式：$$f_i=\sum_{k=0}^{{i-1}v_k\sum_{s_1+s_2+\cdots+s_k=i};;\prod_{j=1}}k f_j$$

我们发现后面这个是一个\(k\)重卷积。那么我们令\(F(x)\)为\(f_i\)的生成函数：$$F(x)=\sum_{k=0}^\infty f_k x^k$$

那么我们根据递归式再加上特殊情况时的值，可以得到：$$F(x)=\sum_{k=0}^\infty v_k F(x)^k+x$$

那么我们发现这就是\(V(x)\)的形式。那么我们就得到：$$F(x)=V(F(x))+x$$

即$$F(x)-V(F(x))=x$$

只要我们令\(G(x)=x-V(x)\)，就可以构造出一个拉格朗日反演的形式：$$G(F(x))=x$$

那么我们作反演就得到：$$[x^{n]F(x)=\frac{1}{n}[x}{n-1}]\left(\frac{x}{G(x)}\right)^n$$

即：$$f_s=\frac{1}{s}[x^{{s-1}]\left(\frac{x}{G(x)}\right)}s$$

注意到我们可以\(x\)和\(G(x)\)约掉一个\(x\)，则我们令：$$H(x)=\sum_{k=0}^\infty v_{k+1} x^k=\frac{C(x)}{x}$$

则有：$$f_s=\frac{1}{s}[x^{{s-1}]\left(\frac{1}{1-H(x)}\right)}n$$

我们直接多项式求逆+多项式求幂就可以解决了。

关于拉格朗日反演、多项式的操作，详见我的这篇博客：多项式全家桶

代码

#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
typedef long long ll;
const ll p=950009857,g=7;
int n,nn,s,m,r[262145];
ll inv[262145],c[262145],gn[2][262145],ans;
inline ll pow(ll a,int b){
	ll ans=1;
	while(b){
		if(b&1)ans=ans*a%p;
		a=a*a%p;
		b>>=1;
	}
	return ans;
}
inline ll add(ll a,ll b){return a+b>p?a+b-p:a+b;}
inline ll cut(ll a,ll b){return a-b<0?a-b+p:a-b;}
void init(){
	for(n=1;n<=s;n<<=1);
	nn=n;
	gn[0][0]=gn[1][0]=1;
	gn[0][1]=pow(g,(p-1)/(n<<1));
	gn[1][1]=pow(gn[0][1],p-2);
	for(int i=2;i<(n<<1);i++){gn[0][i]=gn[0][i-1]*gn[0][1]%p;gn[1][i]=gn[1][i-1]*gn[1][1]%p;}
	inv[1]=1;
	for(int i=2;i<=(n<<1);i++)inv[i]=inv[p%i]*(p-p/i)%p;
}
void NTT(ll c[],int n,int tp=1){
	for(int i=0;i<n;i++){
		r[i]=(r[i>>1]>>1)|((i&1)*(n>>1));
		if(i<r[i])swap(c[i],c[r[i]]);
	}
	for(int i=1;i<n;i<<=1){
		for(int j=0;j<n;j+=(i<<1)){
			for(int k=0;k<i;k++){
				ll x=c[j+k],y=gn[tp!=1][nn/i*k]*c[j+k+i]%p;
				c[j+k]=add(x,y);
				c[j+k+i]=cut(x,y);
			}
		}
	}
}
void INTT(ll c[],int n){
	NTT(c,n,-1);
	for(int i=0;i<n;i++)c[i]=c[i]*inv[n]%p;
}
void inverse(ll c[],int n=n){
	static ll t[262145],tma[262145];
	t[0]=pow(c[0],p-2);
	for(int k=2;k<=n;k<<=1){
		for(int i=0;i<(k<<1);i++)tma[i]=(i<k?c[i]:0);
		for(int i=(k>>1);i<(k<<1);i++)t[i]=0;
		NTT(tma,k<<1);
		NTT(t,k<<1);
		for(int i=0;i<(k<<1);i++)t[i]=cut(add(t[i],t[i]),t[i]*t[i]%p*tma[i]%p);
		INTT(t,k<<1);
	}
	memcpy(c,t,sizeof(ll)*n);
}
void derivative(ll c[],int n=n){for(int i=0;i<n;i++)c[i]=c[i+1]*(i+1)%p;}
void integrate(ll c[],int n=n){for(int i=n-1;i>=1;i--)c[i]=c[i-1]*inv[i]%p;c[0]=0;}
void ln(ll c[],int n=n){
	static ll t[262145];
	for(int i=0;i<(n<<1);i++)t[i]=(i<n?c[i]:0);
	derivative(t,n);
	inverse(c,n);
	NTT(t,n<<1);
	NTT(c,n<<1);
	for(int i=0;i<(n<<1);i++)c[i]=c[i]*t[i]%p;
	INTT(c,n<<1);
	for(int i=n;i<(n<<1);i++)c[i]=0;
	integrate(c,n);
}
void exp(ll c[]){
	static ll t[262145],ta[262145];
	t[0]=1;
	for(int k=2;k<=n;k<<=1){
		for(int i=0;i<(k<<1);i++)ta[i]=t[i];
		ln(ta,k);
		for(int i=0;i<k;i++)ta[i]=cut(c[i],ta[i]);
		ta[0]++;
		NTT(t,k<<1);
		NTT(ta,k<<1);
		for(int i=0;i<(k<<1);i++)t[i]=t[i]*ta[i]%p;
		INTT(t,k<<1);
		for(int i=k;i<(k<<1);i++)t[i]=0;
	}
	memcpy(c,t,sizeof(ll)*n);
}
void pow(ll c[],int k){
	ln(c);
	for(int i=0;i<n;i++)c[i]=c[i]*k%p;
	exp(c);
}
int main(){
	scanf("%d%d",&s,&m);
	for(int i=1;i<=m;i++){
		int x;
		scanf("%d",&x);
		c[x-1]=p-1;
	}
	c[0]=1;
	init();
	inverse(c);
	pow(c,s);
	printf("%lld\n",c[s-1]*inv[s]%p);
}