最短路径问题----Dijkstra算法的解释
先上图:
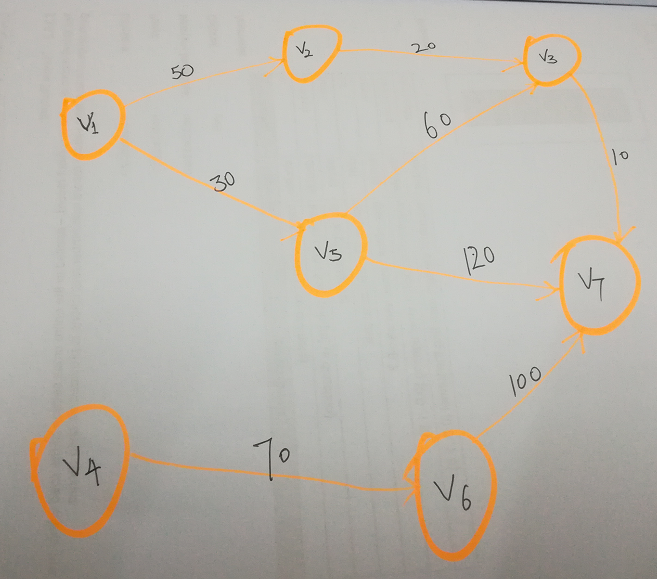
现在要找到地点V1到其余各个地点的最短路径(图中数字的单位默认为km.)。有一个原则是:永远找最小,确保无更小。
第一步:v1->v1,v1->v2,...v1->v7的距离用一维数组dis[0],dis[1],dis[2],...dis[6]表示。初始化数组:dis=[0 50 inf inf 30 inf inf];
第二步:找到dis数组中的最小值(注意不算v1->v1=0),它是dis[4]=30;这个距离就是v1->v5的最小距离了,因为所有的距离都是正数,如果你从v1出发,通过其他顶点绕路绕到v5,那总距离肯定大于30,因为30+(一个大于0的数)肯定大于30.此时,找到了v1->v5的最短路径;
第三步:把顶点v5置为true,代表顶点v5已被访问;
第四步:看v5通往里,从图上可以看到v5通往v3和v7,v5->v3的距离是60,v5->v7的距离是120,所以通过v5中转到v3和v7后,v1->v3的距离变成30+60=90,v1->v7的距离变成30+120=150;这对dis数组中保存的v1到其它各个顶点的距离产生了影响, 此时就用更小的值去更新dis数组中的值。更新后的dis数组是:dis=[0 50 90 inf 30 inf 150].(注:inf代表无穷大)
第五步:找dis数组中除去v1->v5=30这个值之后的最小值,它是v1->v2=50,找到后把顶点v2置为ture.
第六步:从v1出发,通过v2中转,看v2会到达哪里。可以看到,v2->v3=20,这时更新dis数组中v1->v3值,把90更新成70.此时数组dis=[0 50 70 inf 30 inf 150].
第七步:重复第5步,找排除掉顶点是ture的值后,剩余的数的最小值,它是v1->v3=70,把顶点v3置为true.
第八步:从v1出发,通过v3中转,看v3会到达哪里。可以看到,v3->v7=10,这时更新dis数组中v1->v7值,把150更新成80.此时数组dis=[0 50 70 inf 30 inf 80].
第九步:结束!
最终结果:

以下C++代码来源于:https://blog.csdn.net/qq_35644234/article/details/60870719
Dijkstra.h文件的代码:
/************************************************************/
/* 程序作者:Willam */
/* 程序完成时间:2017/3/8 */
/* 有任何问题请联系:2930526477@qq.com */
/************************************************************/
//@尽量写出完美的程序 #pragma once
//#pragma once是一个比较常用的C/C++杂注,
//只要在头文件的最开始加入这条杂注,
//就能够保证头文件只被编译一次。 #include<iostream>
#include<string>
using namespace std; /*
本程序是使用Dijkstra算法实现求解最短路径的问题
采用的邻接矩阵来存储图
*/
//记录起点到每个顶点的最短路径的信息
struct Dis {
string path;
int value;
bool visit;
Dis() {
visit = false;
value = ;
path = "";
}
}; class Graph_DG {
private:
int vexnum; //图的顶点个数
int edge; //图的边数
int **arc; //邻接矩阵
Dis * dis; //记录各个顶点最短路径的信息
public:
//构造函数
Graph_DG(int vexnum, int edge);
//析构函数
~Graph_DG();
// 判断我们每次输入的的边的信息是否合法
//顶点从1开始编号
bool check_edge_value(int start, int end, int weight);
//创建图
void createGraph();
//打印邻接矩阵
void print();
//求最短路径
void Dijkstra(int begin);
//打印最短路径
void print_path(int);
};
Dijkstra.cpp文件的代码:
#include"Dijkstra.h" //构造函数
Graph_DG::Graph_DG(int vexnum, int edge) {
//初始化顶点数和边数
this->vexnum = vexnum;//this 代表调用构造函数的那一个一个对象的地址
this->edge = edge;
//为邻接矩阵开辟空间和赋初值
arc = new int*[this->vexnum];//arc 是二级指针
dis = new Dis[this->vexnum];
for (int i = ; i < this->vexnum; i++) {
arc[i] = new int[this->vexnum];
for (int k = ; k < this->vexnum; k++) {
//邻接矩阵初始化为无穷大
arc[i][k] = INT_MAX;
}
}
}
//析构函数
Graph_DG::~Graph_DG() {
delete[] dis;
for (int i = ; i < this->vexnum; i++) {
delete this->arc[i];
}
delete arc;
} // 判断我们每次输入的的边的信息是否合法
//顶点从1开始编号
bool Graph_DG::check_edge_value(int start, int end, int weight) {
if (start< || end< || start>vexnum || end>vexnum || weight < ) {
return false;
}
return true;
} void Graph_DG::createGraph() {
cout << "请输入每条边的起点和终点(顶点编号从1开始)以及其权重" << endl;
int start;
int end;
int weight;
int count = ;
while (count != this->edge) {
cin >> start >> end >> weight;
//首先判断边的信息是否合法
while (!this->check_edge_value(start, end, weight)) {
cout << "输入的边的信息不合法,请重新输入" << endl;
cin >> start >> end >> weight;
}
//对邻接矩阵对应上的点赋值
arc[start - ][end - ] = weight;
//无向图添加上这行代码
//arc[end - 1][start - 1] = weight;
++count;
}
} void Graph_DG::print() {
cout << "图的邻接矩阵为:" << endl;
int count_row = ; //打印行的标签
int count_col = ; //打印列的标签
//开始打印
while (count_row != this->vexnum) {
count_col = ;
while (count_col != this->vexnum) {
if (arc[count_row][count_col] == INT_MAX)
cout << "∞" << " ";
else
cout << arc[count_row][count_col] << " ";
++count_col;
}
cout << endl;
++count_row;
}
}
void Graph_DG::Dijkstra(int begin){
//首先初始化我们的dis数组
int i;
for (i = ; i < this->vexnum; i++) {
//设置当前的路径
dis[i].path = "v" + to_string(begin) + "-->v" + to_string(i + );
dis[i].value = arc[begin - ][i];
}
//设置起点的到起点的路径为0
dis[begin - ].value = ;
dis[begin - ].visit = true; int count = ;
//计算剩余的顶点的最短路径(剩余this->vexnum-1个顶点)
while (count != this->vexnum) {
//temp用于保存当前dis数组中最小的那个下标
//min记录的当前的最小值
int temp = ;
int min = INT_MAX;
for (i = ; i < this->vexnum; i++) {
if (!dis[i].visit && dis[i].value<min) {
min = dis[i].value;
temp = i;
}
}
//cout << temp + 1 << " "<<min << endl;
//把temp对应的顶点加入到已经找到的最短路径的集合中
dis[temp].visit = true;
++count;
for (i = ; i < this->vexnum; i++) {
//注意这里的条件arc[temp][i]!=INT_MAX必须加,不然会出现溢出,从而造成程序异常
if (!dis[i].visit && arc[temp][i] != INT_MAX && (dis[temp].value + arc[temp][i]) < dis[i].value) {
//如果新得到的边可以影响其他为访问的顶点,那就更新它的最短路径和长度
dis[i].value = dis[temp].value + arc[temp][i];
dis[i].path = dis[temp].path + "-->v" + to_string(i + );
}
}
} }
void Graph_DG::print_path(int begin) {
string str;
str = "v" + to_string(begin);
cout << "以" << str << "为起点的图的最短路径为:" << endl;
for (int i = ; i != this->vexnum; i++) {
if (dis[i].value != INT_MAX)
cout << dis[i].path << "=" << dis[i].value << endl;
else {
cout << dis[i].path << "是无最短路径的" << endl;
}
}
}
main.cpp文件的代码:
#include"Dijkstra.h" //检验输入边数和顶点数的值是否有效,可以自己推算为啥:
//顶点数和边数的关系是:((Vexnum*(Vexnum - 1)) / 2) < edge
bool check(int Vexnum, int edge) {
if (Vexnum <= || edge <= || ((Vexnum*(Vexnum - )) / ) < edge)
return false;
return true;
}
int main() {
int vexnum; int edge; cout << "输入图的顶点个数和边的条数:" << endl;
cin >> vexnum >> edge;
while (!check(vexnum, edge)) {
cout << "输入的数值不合法,请重新输入" << endl;
cin >> vexnum >> edge;
}
Graph_DG graph(vexnum, edge);
graph.createGraph();
graph.print();
graph.Dijkstra();
graph.print_path();
system("pause");
return ;
}
运行结果:
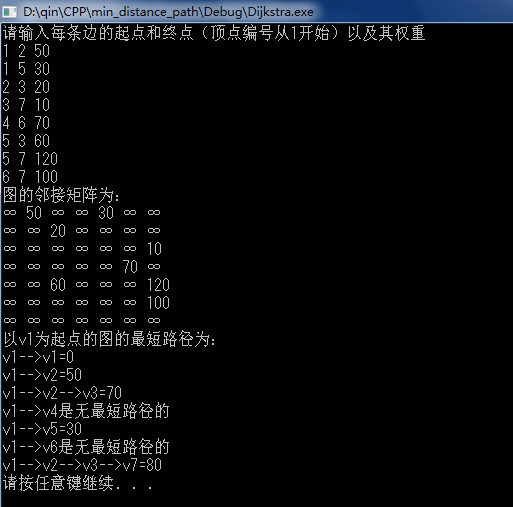
最短路径问题----Dijkstra算法的解释的更多相关文章
- 最短路径 | 深入浅出Dijkstra算法(一)
参考网址: https://www.jianshu.com/p/8b3cdca55dc0 写在前面: 上次我们介绍了神奇的只有五行的 Floyd-Warshall 最短路算法,它可以方便的求得任意两点 ...
- 经典树与图论(最小生成树、哈夫曼树、最短路径问题---Dijkstra算法)
参考网址: https://www.jianshu.com/p/cb5af6b5096d 算法导论--最小生成树 最小生成树:在连通网的所有生成树中,所有边的代价和最小的生成树,称为最小生成树. im ...
- 单源最短路径(dijkstra算法)php实现
做一个医学项目,当中在病例评分时会用到单源最短路径的算法.单源最短路径的dijkstra算法的思路例如以下: 如果存在一条从i到j的最短路径(Vi.....Vk,Vj),Vk是Vj前面的一顶点.那么( ...
- 【算法设计与分析基础】25、单起点最短路径的dijkstra算法
首先看看这换个数据图 邻接矩阵 dijkstra算法的寻找最短路径的核心就是对于这个节点的数据结构的设计 1.节点中保存有已经加入最短路径的集合中到当前节点的最短路径的节点 2.从起点经过或者不经过 ...
- 数据结构与算法--最短路径之Dijkstra算法
数据结构与算法--最短路径之Dijkstra算法 加权图中,我们很可能关心这样一个问题:从一个顶点到另一个顶点成本最小的路径.比如从成都到北京,途中还有好多城市,如何规划路线,能使总路程最小:或者我们 ...
- 【算法导论】单源最短路径之Dijkstra算法
Dijkstra算法解决了有向图上带正权值的单源最短路径问题,其运行时间要比Bellman-Ford算法低,但适用范围比Bellman-Ford算法窄. 迪杰斯特拉提出的按路径长度递增次序来产生源点到 ...
- 最短路径问题---Dijkstra算法详解
侵删https://blog.csdn.net/qq_35644234/article/details/60870719 前言 Nobody can go back and start a new b ...
- 算法学习记录-图——最短路径之Dijkstra算法
在网图中,最短路径的概论: 两顶点之间经过的边上权值之和最少的路径,并且我们称路径上的第一个顶点是源点,最后一个顶点是终点. 维基百科上面的解释: 这个算法是通过为每个顶点 v 保留目前为止所找到的从 ...
- ACM: HDU 3790 最短路径问题-Dijkstra算法
HDU 3790 最短路径问题 Time Limit:1000MS Memory Limit:32768KB 64bit IO Format:%I64d & %I64u Des ...
随机推荐
- Galileo Gen2 之MQTT通讯
前言 原创文章,转载引用务必注明链接.如有疏漏,欢迎斧正. Galileo系统:完整版Yocto,内核版本3.8.7-yocto-standard:宿主机:Windows 7 64 bit 这期主要讲 ...
- 我用select做多路复用踩到的坑
既然说是用select踩到的坑,那么就先直接贴一段使用select的代码上来瞅一下: bool SocketAction(int fd, const char* buf, size_t len, ui ...
- 身份证实名认证接口调用实例(PHP)
基于php的身份证实名认证接口调用代码实例,身份证实名认证接口申请:https://www.juhe.cn/docs/api/id/103 <!--?php // +-------------- ...
- PhoneNumber
项目地址:PhoneNumber 简介:一个获取号码归属地和其他信息(诈骗.骚扰等)的开源库 一个获取号码归属地和其他信息(诈骗.骚扰等)的开源库.支持本地离线(含归属地.骚扰.常用号码)和网络( ...
- merge-sorted-array——合并两个有序数组
Given two sorted integer arrays A and B, merge B into A as one sorted array. Note: You may assume th ...
- 自定义序列化技术3 (.net 序列化技术) C++ 调用C# DLL
打开SerializableAttribute利用里面的函数进行编辑. // sparse.cpp : 定义控制台应用程序的入口点. // #include "stdafx.h" ...
- oauth学习
https://www.cnblogs.com/blowing00/p/4524132.html
- 【puppeteer+Node.js】学习
总结了一下有关puppeteer的学习的网站,以后还会继续更新 puppeteer 介绍 Puppeteer是一个通过DevTools Protocol控制headless chromium的高级no ...
- ubuntu 中文显示乱码问题 (转)
添加中文字符编码: $sudo vim /var/lib/locales/supported.d/local #添加下面的中文字符集 zh_CN.GBK GBK zh_CN.GB2312 GB2312 ...
- Python常用变量处理手记(拼接数字,转json)
1.拼接字符串和数字时,应先把数字做转换 如,bytes(page) 再做拼接:str+page 或者 s = 'abc' print s + str(1) #abc1 使用list和tuple 参考 ...
