【C/C++】函数的分文件编写
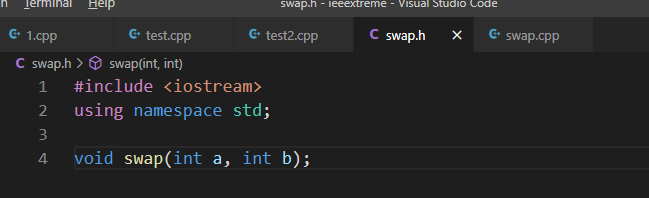
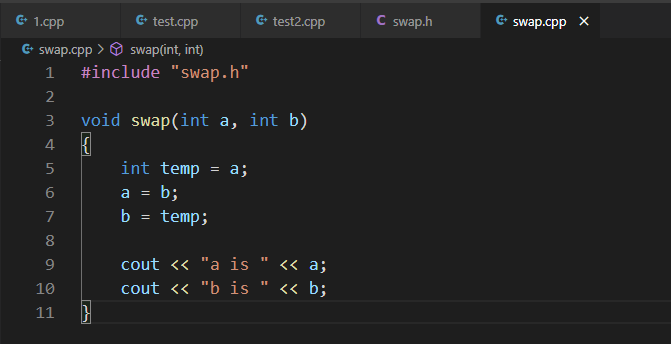
- 创建同名的头文件(.h)和cpp文件。
- 在头文件里写函数声明,在cpp文件中写函数定义。
- 在cpp文件中写#include "xx.h" //自定义头文件名
- 框架(include using namespace std;)写在.h文件中

【C/C++】函数的分文件编写的更多相关文章
- c++类模板分文件编写存在的问题
c++分文件编写的编译机制: 各个文件独立编译,如果在某.cpp文件中出现了函数调用,但是在此.cpp文件并没有对应函数的实现.此时就会在函数调用出生成特定的符号,在之后的链接过程完成函数调用. C+ ...
- c++类模板之分文件编写问题及解决
我们在实际项目中一般习惯头文件(.h)和源文件(.cpp)分开写,这样做的好处良多,但是如果遇到了类模板,这样可能会有一点儿问题. 我们通过一个例子来看: person.h: #pragma once ...
- 【C语言入门教程】5.6 函数库和文件
函数库是为代码复用建立的,将同一类型,需要在不同的程序里使用的函数放置在一起,就组成了一个函数库.如 C 语言的标准库,它集合了开发者常用的函数.开发者自行编写的函数也可以组成函数库,通常称之为自定义 ...
- linux库文件编写入门(笔记)
linux库文件的编写 作者: laomai地址: http://blog.csdn.net/laomai 本文主要参考了如下资料⑴hcj写的"Linux静态/动态链接库的创建和使用&quo ...
- 【Linux技术】linux库文件编写·入门
一.为什么要使用库文件 我们在实际编程中肯定会遇到这种情况:有几个项目里有一些函数模块的功能相同,实现代码也相同,也是我们所说的重复代码.比如,很多项目里都有一个用户验证的功能. 代码段如下: //U ...
- 网站 robots.txt 文件编写
网站 robots.txt 文件编写 Intro robots.txt 是网站根目录下的一个纯文本文件,在这个文件中网站管理者可以声明该网站中不想被robots访问的部分,或者指定搜索引擎只收录指定的 ...
- sort()函数与qsort()函数及其头文件
sort()函数与qsort()函数及其头文件 sort()函数是C++中的排序函数其头文件为:#include<algorithm>头文件: qsort()是C中的排序函数,其头文件为: ...
- atoi()、inet_addr()等函数 time.h文件
1.atoi() 原型:int atoi(const char *nptr); 函数说明:参数nptr字符串,如果第一个非空格字符存在,是数字或者正负号则开始做类型转换,之后检测到非数字(包括结束符 ...
- Linux Makefile文件编写详细步骤与实践
Linux Makefile文件编写详细步骤与实践 1.makefile概述 Windows环境下IDE会帮你完成makefile文件的编写,但在UNIX环境下你就必须自己写makefile了,会不会 ...
随机推荐
- Mybatis:插入数据返回自增主键
使用Mybatis作为工具连接MySQL,要求在插入数据之后返回自增主键 一开始也很迷惑,Mybatis使用insert之后,成功返回的是1,失败会报错或返回0,主键去哪找来 后来知道Mybatis可 ...
- 南京大学OS笔记(1)-应用眼中的操作系统
南京大学OS笔记(1)-应用眼中的操作系统 早就想刷一刷南大JYY老师的os课.之前稍微看过几节,果然讲的风趣幽默,而且现场写代码展示水平确实很高,这次准备认真刷一刷然后好好记一下笔记.当然lab就不 ...
- feignclient各种使用技巧说明
FeignClient常见用法 常规的FeignClient的创建与使用我相信只要使用过spring cloud全家桶的套件的基本上都是非常熟悉了,我们只需定义一个interface,然后定义相关的远 ...
- 大爽Python入门教程 0-3 安装Atom与配置Python环境
大爽Python入门公开课教案 点击查看教程总目录 安装轻量级IDE--Atom 一 下载 下面步骤1,2中网络卡顿的朋友, 请直接查看步骤3来操作 1. 搜索官网 使用搜索引擎搜索Atom, 打开搜 ...
- 菜鸡的Java笔记 第十四 String 类常用方法
/*String 类常用方法 将所有String类的常用方法全部记下来,包括方法名称,参数作用以及类型 一个成熟的编程语言,除了它的语法非常完善之外,那么也需要提供有大量的开发类库 ...
- [loj2478]林克卡特树
原题等价于选择恰好$k+1$条不相交(无公共点)的路径使得边权和最大 证明:对于原题中的最优解,一定包含了k条0边权的边(否则可以将未使用的边删掉,然后将这条路径的末尾与不在同一个连通块内的点连边), ...
- String和其他数据类型
1.String类. 1.1.对String在内存存储方面的理解: 第一:字符串一旦创建不可变. 第二:双引号括起来的字符串存储在字符串常量池中. 第三:字符串的比较必须使用equals方法. 第四: ...
- mabatis的mapper文件找不到-ssm升级maven常见问题
手里项目之前是普通ssm的,打算用业余时间升级一把. 1.首先,搭建好maven的ssm项目. 2.配置好jdk,tomcat环境,先启动. 3.启动没问题后将maven目录结构布置好后直接将原有项目 ...
- 6.K8s集群升级、etcd备份和恢复、资源对象及其yaml文件使用总结、常用维护命令
1.K8s集群升级 集群升级有一定的风险,需充分测试验证后实施 集群升级需要停止服务,可以采用逐个节点滚动升级的方式 1.1 准备新版本二进制文件 查看现在的版本 root@k8-master1:~# ...
- Linux设置默认的声卡
首先查看自己电脑上的声卡 使用命令行查看 orangepi@orangepi3:~$ ll /proc/asound/ total 0 dr-xr-xr-x 4 root root 0 Dec 23 ...
