[leetcode]51. N-QueensN皇后

The n-queens puzzle is the problem of placing n queens on an n×n chessboard such that no two queens attack each other.

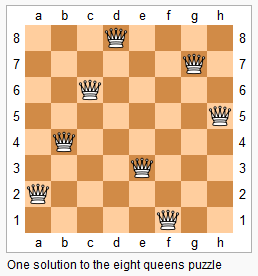
Given an integer n, return all distinct solutions to the n-queens puzzle.

Each solution contains a distinct board configuration of the n-queens' placement, where 'Q' and '.' both indicate a queen and an empty space respectively.

Example:

Input: 4
Output: [
 [".Q..",  // Solution 1
  "...Q",
  "Q...",
  "..Q."],

 ["..Q.",  // Solution 2
  "Q...",
  "...Q",
  ".Q.."]
]
Explanation: There exist two distinct solutions to the 4-queens puzzle as shown above.

题目

NxN棋盘摆N个棋子，要求不能同行、同列、同对角线、同反对角线，返回所有摆法。

思路

DFS： C[i] 表示第i行皇后所在的列编号，即在位置 (i, C[i])上放了一个皇后，这样用一个一维数组，就能记录整个棋盘。

代码

 /*
 TIME: O(n!*n)    n行*每行从n 到 n-1 到 n-2...1  即 n!
 SPACE: O(n)
 */

 class Solution {
       public List<List<String>> solveNQueens(int n) {
         List<List<String>> result = new ArrayList<>();
         int[] C = new int[n]; // C[i]表示第i行皇后所在的列编号，从二维降到一维
         dfs(C, 0, result);
         return result;
     }
     private static void dfs(int[] C, int row, List<List<String>> result) {
         int N = C.length;
         if (row == N) { // 终止条件，也是收敛条件，意味着找到了一个可行解
             List<String> solution = new ArrayList<>();
             // 第i行
             for (int i = 0; i < N; ++i) {
                 char[] charArray = new char[N];
                 Arrays.fill(charArray, '.');
                 //第j列
                 for (int j = 0; j < N; ++j) {
                     if (j == C[i]) charArray[j] = 'Q';
                 }
                 solution.add(new String(charArray));
             }
             result.add(solution);
             return;
         }

         for (int j = 0; j < N; ++j) {  // 扩展状态，一列一列的试
             boolean ok = isValid(C, row, j);
             if (!ok) continue;  // 剪枝，如果非法，继续尝试下一列
             // 执行扩展动作
             C[row] = j;
             dfs(C, row + 1, result);
             // 撤销动作
             // C[row] = -1;
         }
     }

     /**
      * 能否在 (row, col) 位置放一个皇后.
      *
      * @param C 棋局
      * @param row 当前正在处理的行，前面的行都已经放了皇后了
      * @param col 当前列
      * @return 能否放一个皇后
      */
     private static boolean isValid(int[] C, int row, int col) {
         for (int i = 0; i < row; ++i) {
             // 在同一列
             if (C[i] == col) return false;
             // 在同一对角线上
             if (Math.abs(i - row) == Math.abs(C[i] - col)) return false;
         }
         return true;
     }
 }