用Python学分析 - 二项分布

二项分布（Binomial Distribution）
对Bernoulli试验序列的n次序列，结局A出现的次数x的概率分布服从二项分布
- 两分类变量并非一定会服从二项分布
- 模拟伯努利试验中n次独立的重复，每次试验成功的概率为pi

特征值
- 均值（数学期望）和方差：
　　- 不同的值，二项式分布有着不同的形态和偏度值
　　- pi值越大，呈负偏度；pi值越小，呈正偏度
　　- 当 pi = 0.5时，分布是对称的
　　- 当 n * pi 与 n * (1-pi) >= 5 时，样本比例p的抽样分布趋向于正态分布
- 当 n 较大，pi不太极端时，可以采用正态近似方法计算概率分布规律

应用

- 博彩行业的规则设定
- 正常值范围的设定（例：医疗行业）

# 对二项分布概念的理解及计算

 # 对二项分布概念的理解及计算
 
 from scipy.stats import binom
 
 pi = .3; n = 10
 k = 2; m = 8
 
 # 求成功次数为i的概率
 pk = 0
 for i in range(n):
     p = binom( n, pi ).pmf( i )
     if i <= k:
         pk += p
     print( 'P(x = {0:d}) = {1:.4f}'.format( i , p ))
 
 # 求成功小于k次的概率
 print('-'*20)
 p = binom( n, pi ).cdf( k )
 print( 'P(x <= {0:d}) = {1:.4f}'.format( k , p ))
 print( '比较累加值：', pk)
 
 # 求成功大于k次,小于m次的概率
 print('-'*20)
 p = binom( n, pi ).cdf( m ) - binom( n, pi ).cdf( k )
 print( 'P({0:d} < x <= {1:d}) = {2:.4f}'.format( k , m, p ))

运行结果：

# 比较：p对结果的影响

 import numpy as np
 from scipy.stats import binom
 import matplotlib.pyplot as plt
 
 num_trials = 60
 x = np.arange(num_trials)
 
 plt.plot(x, binom(num_trials, 0.2).pmf(x), 'o-', label='p=0.2')
 plt.plot(x, binom(num_trials, 0.5).pmf(x), 'o-', label='p=0.5')
 plt.plot(x, binom(num_trials, 0.7).pmf(x), 'o-', label='p=0.7')
 plt.legend()
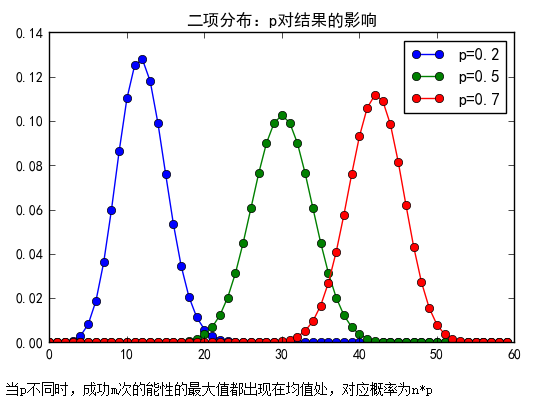
 plt.title( '二项分布：p对结果的影响' )
 plt.show()
 print('当p不同时，成功m次的能性的最大值都出现在均值处，对应概率为n*p')

结果：

# 比较：n对结果的影响

 import numpy as np
 from scipy.stats import binom
 import matplotlib.pyplot as plt
 
 n1 = 10
 n2 = 15
 n3 = 20
 p = 0.5
 x = np.arange( max([n1,n2,n3])+1 )
 
 plt.plot( x, binom.pmf( x, p = 0.5, n = n1), 'o-', label='n=10')
 plt.plot( x, binom.pmf( x, p = 0.5, n = n2), 'o-', label='n=15')
 plt.plot( x, binom.pmf( x, p = 0.5, n = n3), 'o-', label='n=20')
 plt.legend()
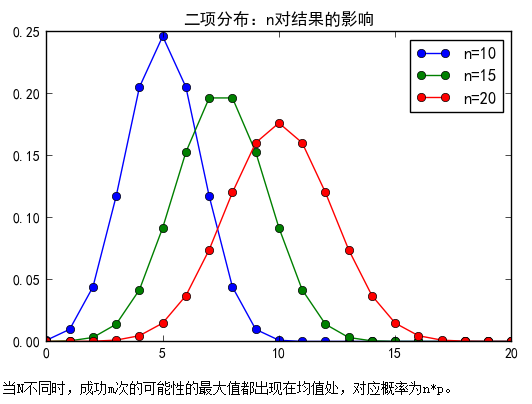
 plt.title( '二项分布：n对结果的影响' )
 plt.show()
 print('当N不同时，成功m次的可能性的最大值都出现在均值处，对应概率为n*p。')

结果：