luogu P3373 【模板】线段树 2

题目描述

如题，已知一个数列，你需要进行下面两种操作：

1.将某区间每一个数加上x

2.将某区间每一个数乘上x

3.求出某区间每一个数的和

输入输出格式

输入格式：

第一行包含三个整数N、M、P，分别表示该数列数字的个数、操作的总个数和模数。

第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。

接下来M行每行包含3或4个整数，表示一个操作，具体如下：

操作1： 格式：1 x y k 含义：将区间[x,y]内每个数乘上k

操作2： 格式：2 x y k 含义：将区间[x,y]内每个数加上k

操作3： 格式：3 x y 含义：输出区间[x,y]内每个数的和对P取模所得的结果

输出格式：

输出包含若干行整数，即为所有操作3的结果。

输入输出样例

输入样例#1：

5 5 38
1 5 4 2 3
2 1 4 1
3 2 5
1 2 4 2
2 3 5 5
3 1 4

输出样例#1：

17
2

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=8，M<=10

对于70%的数据：N<=1000，M<=10000

对于100%的数据：N<=100000，M<=100000

（数据已经过加强^_^）

样例说明：

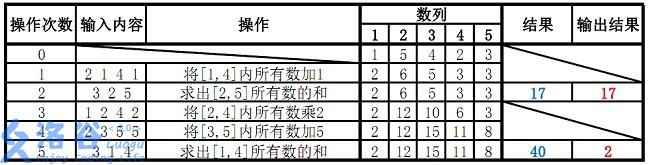
故输出应为17、2（40 mod 38=2）

---

需要越来越习惯lazy-tag的使用才行啊

tag1表示乘，tag2表示加

线段树的写法真是各有各的风格    大雾

 #include<cstdio>
 #include<cstring>
 #include<iostream>
 using namespace std;

 typedef long long ll;

 inline int read(){
     char ch;
     int re=;
     bool flag=;
     while((ch=getchar())!='-'&&(ch<''||ch>''));
     ch=='-'?flag=:re=ch-'';
     while((ch=getchar())>=''&&ch<='')  re=re*+ch-'';
     return flag?-re:re;
 }

 struct segment{
     int l,r;
     ll sum,tag1,tag2;
     segment(){
         sum=;
         tag1=;
         tag2=;
     }
 };

 const int maxn=;

 int cnt,n,m;
 ll mod;
 segment tre[maxn<<];
 int data[maxn];

 inline void push_up(int x){
     tre[x].sum=(tre[x<<].sum+tre[x<<|].sum)%mod;
 }

 void build(int x,int l,int r){
     tre[x].l=l;  tre[x].r=r;
     if(l==r){
         tre[x].sum=data[l];
         return;
     }
     int mid=(l+r)>>;
     build(x<<,l,mid);  build(x<<|,mid+,r);
     push_up(x);
 }

 void init(){
     n=read();  m=read();  mod=read();
     for(int i=;i<=n;i++)  data[i]=read();
     build(,,n);
 }

 inline void push_down(int x){
     int lson=x<<,rson=lson|;

     if(tre[x].tag1!=){
         tre[lson].tag1=(tre[lson].tag1*tre[x].tag1)%mod;
         tre[rson].tag1=(tre[rson].tag1*tre[x].tag1)%mod;
         tre[lson].tag2=(tre[lson].tag2*tre[x].tag1)%mod;
         tre[rson].tag2=(tre[rson].tag2*tre[x].tag1)%mod;
         tre[lson].sum=(tre[lson].sum*tre[x].tag1)%mod;
         tre[rson].sum=(tre[rson].sum*tre[x].tag1)%mod;
         tre[x].tag1=;
     }

     if(tre[x].tag2){
         tre[lson].tag2=(tre[lson].tag2+tre[x].tag2)%mod;
         tre[lson].sum=(tre[lson].sum+tre[x].tag2*(tre[lson].r-tre[lson].l+))%mod;
         tre[rson].tag2=(tre[rson].tag2+tre[x].tag2)%mod;
         tre[rson].sum=(tre[rson].sum+tre[x].tag2*(tre[rson].r-tre[rson].l+))%mod;
         tre[x].tag2=;
     }
 }

 void update_add(int x,int L,int R,int c){
     if(L<=tre[x].l&&tre[x].r<=R){
         tre[x].tag2=(tre[x].tag2+c)%mod;
         tre[x].sum=(tre[x].sum+c*(tre[x].r-tre[x].l+))%mod;
         return;
     }

     int mid=(tre[x].l+tre[x].r)>>;
     if(tre[x].tag1!=||tre[x].tag2)  push_down(x);
     if(R<=mid)  update_add(x<<,L,R,c);
     else  if(L>mid)  update_add(x<<|,L,R,c);
     else{  update_add(x<<,L,mid,c);  update_add(x<<|,mid+,R,c);  }
     push_up(x);
 }

 void update_mul(int x,int L,int R,int c){
     if(L<=tre[x].l&&tre[x].r<=R){
         tre[x].tag1=(tre[x].tag1*c)%mod;
         tre[x].tag2=(tre[x].tag2*c)%mod;
         tre[x].sum=(tre[x].sum*c)%mod;
         return;
     }

     int mid=(tre[x].l+tre[x].r)>>;
     if(tre[x].tag1!=||tre[x].tag2)  push_down(x);
     if(R<=mid)  update_mul(x<<,L,R,c);
     else  if(L>mid)  update_mul(x<<|,L,R,c);
     else{  update_mul(x<<,L,mid,c);  update_mul(x<<|,mid+,R,c);  }
     push_up(x);
 }

 ll query_sum(int x,int L,int R){
     if(L<=tre[x].l&&tre[x].r<=R){
         return tre[x].sum;
     }
     if(tre[x].tag1!=||tre[x].tag2)  push_down(x);
     int mid=(tre[x].l+tre[x].r)>>;
     if(R<=mid)  return query_sum(x<<,L,R);
     if(L>mid)  return query_sum(x<<|,L,R);
     return (query_sum(x<<,L,mid)+query_sum(x<<|,mid+,R))%mod;
 }

 void solve(){
     int opt,L,R,c;
     for(int i=;i<m;i++){
         opt=read();
         switch(opt){
             case :{
                 L=read();  R=read();  c=read();
                 update_mul(,L,R,c);
                 break;
             }
             case :{
                 L=read();  R=read();  c=read();
                 update_add(,L,R,c);
                 break;
             }
             case :{
                 L=read();  R=read();
                 printf("%lld\n",query_sum(,L,R));
                 break;
             }
         }
     }
 }

 int main(){
     //freopen("temp.in","r",stdin);
     init();
     solve();
     return ;
 }

---

她的话不多但笑起来是那么平静优雅

她柔弱的眼神里装的是什么 是思念的忧伤