PAT_A1123#Is It a Complete AVL Tree

Source:

PAT A1123 Is It a Complete AVL Tree (30 分)

Description:

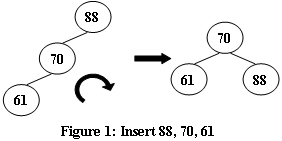
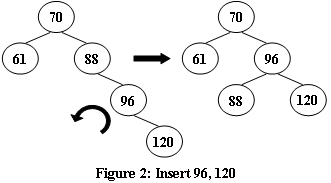
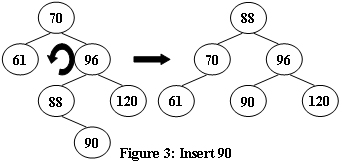
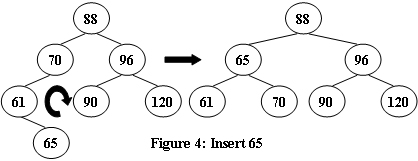
An AVL tree is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Figures 1-4 illustrate the rotation rules.

Now given a sequence of insertions, you are supposed to output the level-order traversal sequence of the resulting AVL tree, and to tell if it is a complete binary tree.

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer N (≤ 20). Then N distinct integer keys are given in the next line. All the numbers in a line are separated by a space.

Output Specification:

For each test case, insert the keys one by one into an initially empty AVL tree. Then first print in a line the level-order traversal sequence of the resulting AVL tree. All the numbers in a line must be separated by a space, and there must be no extra space at the end of the line. Then in the next line, print YES if the tree is complete, or NO if not.

Sample Input 1:

5
88 70 61 63 65

Sample Output 1:

70 63 88 61 65
YES

Sample Input 2:

8
88 70 61 96 120 90 65 68

Sample Output 2:

88 65 96 61 70 90 120 68
NO

Keys:

• 二叉树的建立
• 二叉树的遍历
• 完全二叉树（Complete Binary Tree）
• 平衡二叉树（Self-balancing Binary Search Tree，AVL tree）

Attention:

• 判断完全二叉树，while的固定写法
• Rotation中，先Update root，再Update temp，否则会影响结果，注意

Code:

 /*
 Data: 2019-06-24 15:36:45
 Problem: PAT_A1123#Is It a Complete AVL Tree
 AC: 35:46

 题目大意：
 由插入序列构造一棵AVL树，输出层次遍历并判断是否为一棵完全二叉树

 基本思路：
 构造平衡二叉树，
 中序遍历并判断是否为完全二叉树
 */
 #include<cstdio>
 #include<queue>
 #include<algorithm>
 using namespace std;
 struct node
 {
     int data;
     int height;
     node *lchild, *rchild;
 };

 int GetHeight(node *root)
 {
     if(root == NULL)
         return ;
     else
         return root->height;
 }

 int GetBalanceFactor(node *root)
 {
     return GetHeight(root->lchild) - GetHeight(root->rchild);
 }

 void UpdataHeight(node *&root)
 {
     root->height = max(GetHeight(root->lchild),GetHeight(root->rchild))+;
 }

 void LeftRotation(node *&root)
 {
     node *temp = root->rchild;
     root->rchild = temp->lchild;
     temp->lchild = root;
     UpdataHeight(root);
     UpdataHeight(temp);
     root = temp;
 }

 void RightRotation(node *&root)
 {
     node *temp = root->lchild;
     root->lchild = temp->rchild;
     temp->rchild = root;
     UpdataHeight(root);
     UpdataHeight(temp);
     root = temp;
 }

 void Insert(node *&root, int x)
 {
     if(root == NULL)
     {
         root = new node;
         root->data = x;
         root->height=;
         root->lchild = root->rchild = NULL;
     }
     else if(x < root->data)
     {
         Insert(root->lchild, x);
         UpdataHeight(root);
         if(GetBalanceFactor(root) == )
         {
             if(GetBalanceFactor(root->lchild) == )
                 RightRotation(root);
             else
             {
                 LeftRotation(root->lchild);
                 RightRotation(root);
             }
         }
     }
     else
     {
         Insert(root->rchild, x);
         UpdataHeight(root);
         if(GetBalanceFactor(root) == -)
         {
             if(GetBalanceFactor(root->rchild) == -)
                 LeftRotation(root);
             else
             {
                 RightRotation(root->rchild);
                 LeftRotation(root);
             }
         }
     }
 }

 int IsComplete(node *root, int n)
 {
     queue<node*> q;
     q.push(root);
     int cnt=, ans=;
     while(!q.empty())
     {
         root = q.front();
         q.pop();
         if(root)
         {
             printf("%d%c", root->data,++cnt==n?'\n':' ');
             q.push(root->lchild);
             q.push(root->rchild);
         }
         else
         {
             if(cnt==n)
                 break;
             else
             {
                 ans=;
                 while(!q.empty())
                 {
                     root = q.front();
                     if(root) break;
                     else   q.pop();
                 }
             }
         }
     }
     return ans;
 }

 int main()
 {
 #ifdef ONLINE_JUDGE
 #else
     freopen("Test.txt", "r", stdin);
 #endif // ONLINE_JUDGE

     int n,x;
     node *root = NULL;
     scanf("%d", &n);
     for(int i=; i<n; i++)
     {
         scanf("%d", &x);
         Insert(root, x);
     }
     if(IsComplete(root, n))
         printf("YES");
     else
         printf("NO");

     return ;
 }