算法导论 第十二章 二叉搜索树（python）

上图：

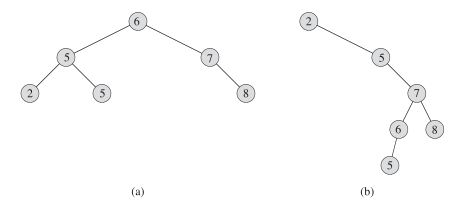
这是二叉搜索树（也有说是查找树的）基本结构：如果y是x的左子树中的一个结点，那么y.key <= x.key(如a图中的6根结点大于它左子树的每一个结点 6 >= {2,5,5}),如果y是x的右子树中的一个结点，那么y.key >x.key

注：不同堆，堆是中间的结点最大或最小，而二叉搜索树是左中右的大小顺序，我们用这个特性来遍历二叉搜索树得到是他的顺序排列（中序遍历）#中在什么地方就叫什么遍历 如前序遍历：中左右  后序：左右中

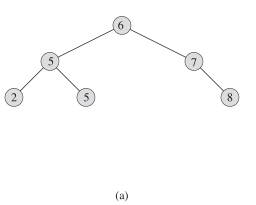
如图a他的中序遍历为 2->5->5->6->7->8 #从大到小

基本操作：

SEARCH：查找关键字为k的结点  O(h) #h为二叉树的高度

MINIMUM:查找二叉树的最小值（显然是最左的那个结点） O(h)

MAXIMUM:查找二叉树的最大值（显然是最右的那个结点） O(h)

PREDECESSOR:查找x的前驱y O(h)

SUCCESSOR:查找x的后驱y O(h)

INSERT:插入结点z O(h)

DELETE:删除结点z O(h)

注：

1.其中插入和删除因为要调整树的结构所以有点复杂

2.复杂都为O(h) #h为二叉树的高度,我们看下图

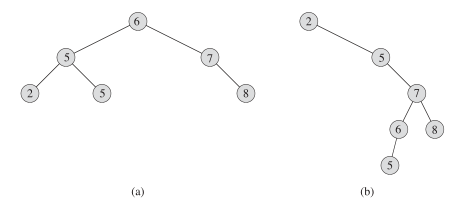
他们的结点数（n）都是6但是高度是不同的 ha = 2 而 hb = 4 ，这种差距在应用中可能会有很大的性能问题，同以前的快速排序一样使用随机化方法或者是其他的限定条件（如红黑树）来保证性能在一个好一点的范围内（h = logn），就是不能让二叉树保持一条直线向下

给出python实现：

 class Node: #结点

     def __init__(self,data):
         self.left = None
         self.right = None
         self.parent = None
         self.data = data
     def createNode(self,data):
         #初始化
         return Node(data)

     def inorder_tree_walk(self):
         """
         中序遍历
         """
         if self.left: #左
             self.left.inorder_tree_walk()
         print(self.data,end = ' ') #中
         if self.right: #右
             self.right.inorder_tree_walk()
     def tree_search(self,data):
         if self == None or self.data == data:
             return self

         if data < self.data:
             return self.left.tree_seatch(data)
         else :
             return self.right.tree_seatch(data)

     def iterative_tree_search(self,data):
         #非递归版查找一般会比递归版更快
         n = self
         while n != None and data != n.data:
             if data < n.data:
                 n = n.left
             else:
                 n = n.right
         return n

     def tree_mininum(self):
         if self.left:
             return self.left.tree_mininum()
         else:
             return self

     def tree_maximun(self):
         if self.right:
             return self.right.true_maximun()
         else:
             return self

     def tree_successor(self):

         """
         找后继：
         有右子树，取右子树中最小的
         没有右子树，也就是这个子树中最大的，应该向上找第一个把他当右子树的结点
         前驱 相反
         """
         x = self
         if x.right != None:
             return x.right.tree_mininum()
         else:
             p = x.parent
             while p and p.right == x:
                 x = p
                 p = p.parent
             return p
     def tree_predecessor(self):
         x = self
         if x.left != None:
             return x.left.tree_maximun()
         else:
             p = x.parent
             while p and p.left == x:
                 x = p
                 p = p.parent
             return p

     def tree_insert(self,data):
         #插入data
         node = self
         while node:
             if data < node.data:
                 next = node.left
             else:
                 next = node.right
             if next:
                 node = next
             else:
                 break
         nn = self.createNode(data)
         if data < node.data:
             node.left = nn
             node.left.parent = node
         else:
             node.right = nn
             node.right.parent = node
         return nn

     def tree_delete(self,root):
         '''
         1.有2子树
             1.相对树结构移除的是self

         2.少于有2子树
             1.相对树结点移除的是self的后继 当然删除还是self.data
         '''

         n = self

         if n.left == None or n.right == None :
             y = n #至多有1子树直接删除
         else:
             y = n.tree_successor()#要用后继覆盖他

         if y.left == None: #x 覆盖 y #至多有1个子树  y是黑的话 x的黑+1
             x = y.right
         else:
             x = y.left

         x.parent = y.parent
         if y.parent == None:
             root = x
         elif y == y.parent.left:
             y.parent.left = x
         else:
             y.parent.right = x

         if y != n:
             n.data = y.data
         return root;

 if __name__ == '__main__':
     root = Node(6)
     root.tree_insert(5)
     root.tree_insert(7)
     root.tree_insert(2)
     root.tree_insert(3)
     root.tree_insert(8)
     print("中序遍历: ",end = '')
     root.inorder_tree_walk()
     print("\n查找：",end = '')
     test1= root.iterative_tree_search(5)
     print(str(test1.data)+'的后继：'+str(test1.tree_successor().data))

     print("查找：",end = '')
     test2= root.tree_search(6)
     print(str(test2.data)+'的前驱：'+str(test2.tree_predecessor().data))
     root = test2.tree_delete(root)
     print("删除6后：",end = '')
     root.inorder_tree_walk()
     root = root.iterative_tree_search(2).tree_delete(root)
     print("\n删除2后：",end = '')
     root.inorder_tree_walk()
 '''
 ================= RESTART: F:\python\algorithms\12_1_tree.py =================
 中序遍历: 2 3 5 6 7 8
 查找：5的后继：6
 查找：6的前驱：5
 删除6后：2 3 5 7 8
 删除2后：3 5 7 8
 >>> 

 python 3.5.1 win7
 '''                                                   

参考引用：

http://www.wutianqi.com/?cat=515&paged=4

http://blog.csdn.net/fxjtoday/article/details/6448083