题解报告：CODE[VS] 1082 线段树练习3（区间修改+区间查询）

题目描述 Description

给你N个数，有两种操作：

1：给区间[a,b]的所有数增加X

2：询问区间[a,b]的数的和。

输入描述 Input Description

第一行一个正整数n，接下来n行n个整数，

再接下来一个正整数Q，每行表示操作的个数，

如果第一个数是1，后接3个正整数，

表示在区间[a,b]内每个数增加X,如果是2，

表示操作2询问区间[a,b]的和是多少。

pascal选手请不要使用readln读入

输出描述 Output Description

对于每个询问输出一行一个答案

样例输入 Sample Input

3

1

2

3

2

1 2 3 2

2 2 3

样例输出 Sample Output

9

数据范围及提示 Data Size & Hint

数据范围

1<=n<=200000

1<=q<=200000

解题思路：题目虽然写的是线段树，但是很多情况下树状数组都可以代替线段树来做，而且有一个很明显的优点就是树状数组的代码要比线段树简洁得多，因此拿这道题作为树状数组区间修改+区间查询入门最好不过了！（这里不涉及线段树代码，不会线段树的另百度自学）上一篇博文里讲到用差分数组实现区间修改，但是怎么实现区间查询呢？联系单点查询求前缀和公式易得求区间[1,p]内所有元素和的公式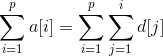：。从中可以发现：等式右边的式子中d[1]被加了p次，d[2]被加了p-1次...，于是位置p的前缀和公式为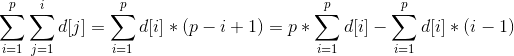：，将其展开可以得到a[1]+a[2]+...+a[p]=(d[1])+(d[1]+d[2])+...+(d[1]+d[2]+...+d[p])=p*(d[1]+d[2]+...+d[p])-(0*d[1]+1*d[2]+...+(p-1)*d[p])，看到没，是不是和单点查询树状数组维护差分数组一样？接下来我们只需用两个树状数组来维护一下两个差分数组：sum1[i]=d[i]，sum2[i]=(i-1)*d[i]。区间修改：假设将区间[l,r]中每个元素加上k，则只需在两个树状数组上进行修改：sum1[l]+=k，sum1[r+1]-=k，sum2[l]+=(l-1)*k，sum2[r+1]-=r*k，然后区间[1,p]的求和公式（区间查询）就为p*get_sum(sum1,p)-get_sum(sum2,p)。以上所有操作的时间复杂度均为O(nlogn)，显然比线段树快且简洁多了。

AC代码(542ms)：

 /*
 作者:霜雪千年
 题目:p1082 线段树练习 3
 */

 #include<bits/stdc++.h>
 using namespace std;
 typedef long long LL;
 const int maxn=2e5+;
 LL n,l,r,k,q,p,val[maxn],sum1[maxn],sum2[maxn];
 void add(LL *sum,LL x,LL val){
     while(x<=n){sum[x]+=val;x+=(x&-x);}
 }
 LL get_sum(LL *sum,LL x){
     LL ans=;
     while(x>){ans+=sum[x];x-=(x&-x);}
     return ans;
 }
 LL ask(LL x){
     return x*get_sum(sum1,x)-get_sum(sum2,x);
 }
 int main(){
     while(~scanf("%lld",&n)){
         memset(sum1,,sizeof(sum1));//注意清0
         memset(sum2,,sizeof(sum2));
         memset(val,,sizeof(val));
         for(LL i=;i<=n;++i){
             scanf("%lld",&val[i]);
             add(sum1,i,val[i]-val[i-]);//维护两个差分数组
             add(sum2,i,(i-)*(val[i]-val[i-]));
         }
         scanf("%lld",&q);
         while(q--){
             scanf("%lld",&p);
             if(p==){
                 scanf("%lld%lld%lld",&l,&r,&k);
                 add(sum1,l,k),add(sum1,r+,-k);//区间修改
                 add(sum2,l,(l-)*k);add(sum2,r+,-r*k);
             }
             else{
                 scanf("%lld%lld",&l,&r);
                 printf("%lld\n",ask(r)-ask(l-));//区间查询[1,r]-[1,l-1]=[l,r]
             }
         }
     }
     return ;
 }