HDU 3714/UVA1476 Error Curves

Error Curves

Time Limit: 4000/2000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 4137    Accepted Submission(s): 1549

Problem Description

Josephina is a clever girl and addicted to Machine Learning recently. She
pays much attention to a method called Linear Discriminant Analysis, which
has many interesting properties.
In order to test the algorithm's efficiency, she collects many datasets.
What's more, each data is divided into two parts: training data and test
data. She gets the parameters of the model on training data and test the
model on test data. To her surprise, she finds each dataset's test error curve is just a parabolic curve. A parabolic curve corresponds to a quadratic function. In mathematics, a quadratic function is a polynomial function of the form f(x) = ax2 + bx + c. The quadratic will degrade to linear function if a = 0.

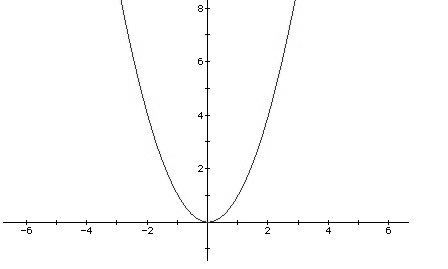
It's very easy to calculate the minimal error if there is only one test error curve. However, there are several datasets, which means Josephina will obtain many parabolic curves. Josephina wants to get the tuned parameters that make the best performance on all datasets. So she should take all error curves into account, i.e., she has to deal with many quadric functions and make a new error definition to represent the total error. Now, she focuses on the following new function's minimum which related to multiple quadric functions. The new function F(x) is defined as follows: F(x) = max(Si(x)), i = 1...n. The domain of x is [0, 1000]. Si(x) is a quadric function. Josephina wonders the minimum of F(x). Unfortunately, it's too hard for her to solve this problem. As a super programmer, can you help her?

 

Input

The input contains multiple test cases. The first line is the number of cases T (T < 100). Each case begins with a number n (n ≤ 10000). Following n lines, each line contains three integers a (0 ≤ a ≤ 100), b (|b| ≤ 5000), c (|c| ≤ 5000), which mean the corresponding coefficients of a quadratic function.

 

Output

For each test case, output the answer in a line. Round to 4 digits after the decimal point.

 

Sample Input

2
1
2 0 0
2
2 0 0
2 -4 2

 

Sample Output

0.0000

0.5000

 

Author

LIN, Yue

 

大致图像是一堆一二次函数相交，取上面一层的函数，然后把这些分段函数和在一起得到F(x)，求F(x)的最小值

/* ***********************************************
Author        :pk28
Created Time  :2015/8/22 16:15:00
File Name     :4.cpp
************************************************ */
#include <iostream>
#include <cstring>
#include <cstdlib>
#include <stdio.h>
#include <algorithm>
#include <vector>
#include <queue>
#include <set>
#include <map>
#include <string>
#include <math.h>
#include <stdlib.h>
#include <iomanip>
#include <list>
#include <deque>
#include <stack>
#define ull unsigned long long
#define ll long long
#define mod 90001
#define INF 0x3f3f3f3f
#define maxn 10000+10
#define cle(a) memset(a,0,sizeof(a))
const ull inf = 1LL << ;
const double eps=1e-;
using namespace std;
struct node{
    double a,b,c;
}nod[maxn];
int n;
bool cmp(int a,int b){
    return a>b;
}
double check(double x){
    double Max=-INF;
    for(int i=;i<=n;i++){
        double tmp=nod[i].a*x*x+nod[i].b*x+nod[i].c;
        if(tmp>Max)Max=tmp;
    }
    return Max;
}
int main()
{
    #ifndef ONLINE_JUDGE
    freopen("in.txt","r",stdin);
    #endif
    //freopen("out.txt","w",stdout);
    int t;
    cin>>t;
    while(t--){
        cin>>n;
        for(int i=;i<=n;i++){
            scanf("%lf%lf%lf",&nod[i].a,&nod[i].b,&nod[i].c);
        }
        double mid,mmid,l=0.0,r=1000.0,ans;
        while(r-l>eps){
            mid=(l+r)/,;
            mmid=(mid+r)/2.0;
            double t1=check(mid);
            double t2=check(mmid);
            if(t1<t2){
                ans=t1;
                r=mmid;
            }
            else{
                ans=t2;
                l=mid;
            }
        }
        printf("%.4lf\n",ans);
    }
    return ;
}

精度1e-9  1e-10