hdu4115：Eliminate the Conflict

n<=10000局剪刀石头布，对面第i局出Ai，m<=10000种对你出什么提出的要求：Xi Yi Wi 表示第Xi局和第Yi局，Wi=1:必须不同；Wi=0:必须相同，问是否存在你一局都不能输的可行解。

一开始对面就把你每局的选择减成2个了，又是一个2-SAT问题。至于建图一定要考虑周全！注意一个条件对Xi和Yi带来的影响都要考虑！

A和B必须不同：

A和B必须相同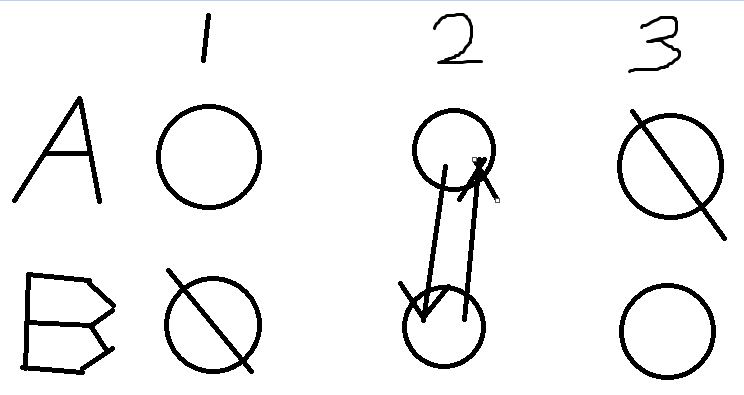：错误！未考虑清楚“必须相同”的含义，就是说，如果B没有一样的，那么A这个就不能选！

那么还要把这些不能选的点删掉吗？看了大神博客，发现神奇姿势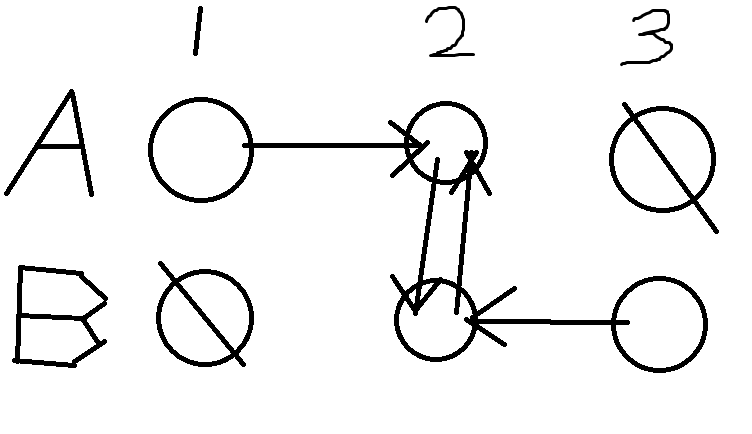：这样A1和B3就永远不可能选了，因为一旦选立刻出现矛盾。

注意事项：由于建边过程繁琐，中途思路混乱WA了一次。注意检查！！！

 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<cstdlib>
 #include<cmath>
 //#include<iostream>
 using namespace std;

 int n,m,T;
 #define maxn 10011*2
 #define maxe 10011*4
 struct Edge{int to,next;};
 struct Graph
 {
     Edge edge[maxe];int le;
     int first[maxn],vis[maxn];
     void clear()
     {
         le=;
         memset(first,,sizeof(first));
     }
     void insert(int x,int y)
     {
         edge[le].to=y;
         edge[le].next=first[x];
         first[x]=le++;
     }
     int sta[maxn],top;
     bool dfs(int x)
     {
         if (vis[x^]) return ;
         if (vis[x]) return ;
         vis[x]=;
         sta[++top]=x;
         for (int i=first[x];i;i=edge[i].next)
             if (!dfs(edge[i].to)) return ;
         return ;
     }
     bool twosat()
     {
         memset(vis,,sizeof(vis));
         for (int i=;i<=n;i++)
             if (!vis[i*] && !vis[i*+])
             {
                 top=;
                 if (!dfs(i*))
                 {
                     for (;top;top--) vis[sta[top]]=;
                     if (!dfs(i*+)) return ;
                 }
             }
         return ;
     }
 }G;
 struct Point
 {
     int a,b;
 }game[maxn];
 int x,y,w;
 int main()
 {
     scanf("%d",&T);
     for (int t=;t<=T;t++)
     {
         scanf("%d%d",&n,&m);
         for (int i=;i<=n;i++)
         {
             scanf("%d",&x);
             if (x==) {game[i].a=;game[i].b=;}
             if (x==) {game[i].a=;game[i].b=;}
             if (x==) {game[i].a=;game[i].b=;}
         }
         G.clear();
         for (int i=;i<=m;i++)
         {
             scanf("%d%d%d",&x,&y,&w);
             if (w)
             {
                 if (game[x].a==game[y].a)
                 {
                     G.insert(x*,y*+);
                     G.insert(y*,x*+);
                 }
                 if (game[x].a==game[y].b)
                 {
                     G.insert(x*,y*);
                     G.insert(y*+,x*+);
                 }
                 if (game[x].b==game[y].a)
                 {
                     G.insert(x*+,y*+);
                     G.insert(y*,x*);
                 }
                 if (game[x].b==game[y].b)
                 {
                     G.insert(x*+,y*);
                     G.insert(y*+,x*);
                 }
             }
             else
             {
                 if (game[x].a==game[y].a)
                 {
                     G.insert(x*,y*);
                     G.insert(y*,x*);
                 }
                 else if (game[x].a==game[y].b)
                 {
                     G.insert(x*,y*+);
                     G.insert(y*+,x*);
                 }
                 else G.insert(x*,x*+);
                 if (game[x].b==game[y].a)
                 {
                     G.insert(x*+,y*);
                     G.insert(y*,x*+);
                 }
                 else if (game[x].b==game[y].b)
                 {
                     G.insert(x*+,y*+);
                     G.insert(y*+,x*+);
                 }
                 else G.insert(x*+,x*);
                 if (game[y].a!=game[x].a && game[y].a!=game[x].b)
                     G.insert(y*,y*+);
                 if (game[y].b!=game[x].a && game[y].b!=game[x].b)
                     G.insert(y*+,y*);
             }
         }
         printf("Case #%d: ",t);
         if (G.twosat()) printf("yes");else printf("no");
         puts("");
     }
     return ;
 }