2018 ICPC 沈阳网络预赛 Fantastic Graph （优先队列）

【传送门】https://nanti.jisuanke.com/t/31447

【题目大意】：有一个二分图，问能不能找到它的一个子图，使得这个子图中所有点的度数在区间【L,R】之内。

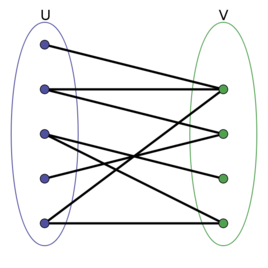
【题解】首先我们分这几种情况讨论：

（1）如果集合U,V中存在某个点，它的度数小于L，那么肯定就不满足题意，直接输出No。所以对任意i, degree[i] >= L

（2）如果集合U,V中所有点的度数都在给定区间内，直接输出Yes。

（3）如果集合U,V中存在某些点的度数大于R，则需要减少与它关联的边，直到它的度数小于等于R

那么如何删边呢？我们把某个度数过大的点X的所有终点放入优先队列中，这个队列根据点的度数排好序，度数大的点Y在队首，当X的度数大于R时，我们取出队首Y，如果Y度数大于L，代表可以删边，X,Y的度数均自减1。

如果X的度数大于R时，队首Y的度已经不能再减（已经小于等于L了），那么就表明找不到这样的子图，输出No。

把所有的点都按照上述过程扫一遍，看中途是不是会判定找不到这样的子图。

时间复杂度：O（N*LogN）

有网上题解说可以使用网络流，暂时记下以后再探讨。

【AC代码】

#include <queue>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
const int maxn = ;
vector<int> G[maxn];//存图
int offset = ;//两个集合标号都从1开始为了区分设置一个偏移量，右边的序号都加上偏移量
int degree[maxn];//存度数 

// 自定义优先级  按度优先
struct cmp
{
    bool operator()(const int &t1,const int &t2)
    {
        return degree[t1] < degree[t2];
    }
};

//初始化
void init(){
    memset(degree , , sizeof degree);
    for(int i=; i<maxn; i++)    G[i].clear();
}

int main(){
    int n,m,k;
    int l,r;
    int u,v;
    int ca = ;
    while(scanf("%d %d %d", &n,&m,&k) != EOF){
        init();
        int flag = ;
        scanf("%d %d",&l, &r);
        //建图，记录度数
        for(int i=; i<=k; i++){
            scanf("%d %d",&u, &v);
            G[u].push_back(v+offset);
            G[v+offset].push_back(u);
            degree[u]++;
            degree[v+offset]++;
        }
        //只要有一个点度数小于L就GG
        for(int i= ; i<=n; i++){
        //    cout<<" "<<degree[i]<<endl;
            if(degree[i] < l){
                flag = ;
                break;
            }
        }
        for(int i=+offset; i<=m+offset; i++){
        //    cout<<" "<<degree[i]<<endl;
            if(degree[i] < l){
                flag = ;
                break;
            }
        }
        if(!flag){
            printf("Case %d: No\n" , ca++);
            continue;
        }

        //开始执行步骤（3） 对左边集合所有点  删边减度
        for(int i=; i<=n; i++){
            if(flag == )    break;

             priority_queue<int,vector<int>,cmp> q; //定义优先队列
             while(!q.empty()) q.pop();

             //对每一个点X的终点入队等待删边
             for(int j=; j<G[i].size(); j++){
                 q.push(G[i][j]);
            }
            //只要这个点 X的度数大于R必须删边减度
            while(degree[i] > r){
                int f = ;
                //取出队首
                int tp = q.top();
                int t = degree[tp];
                q.pop();
                if(t- >= l){
                    f = ;
                    degree[tp] --;
                    degree[i]--;

                }else{
                    f = ;
                }
                if(degree[tp] >= l+)
                    q.push(tp);
                if(f == ){
                    flag = ;
                    break;
                }
            }
        }

        //一样的操作，对右边集合
        for(int i=+offset; i<=m+offset; i++){
            if(flag == )    break;
             priority_queue<int,vector<int>,cmp> q;
             while(!q.empty()) q.pop();

             for(int j=; j<G[i].size(); j++){
                 q.push(G[i][j]);
            }

            while(degree[i] > r){
                int f = ;
                int tp = q.top();
                int t = degree[tp];
                q.pop();
                if(t- >= l){
                    f = ;
                    degree[tp] --;
                    degree[i]--;

                }
                if(degree[tp] >= l+)
                    q.push(tp);
                if(f == ){
                    flag = ;
                    break;
                }
            }
        }

        ///最终判定
        if(flag)    printf("Case %d: Yes\n" , ca++);
        else    printf("Case %d: No\n" , ca++);    

    }
}