POJ-3436 ACM Computer Factory（网络流EK）

As you know, all the computers used for ACM contests must be identical, so the participants compete on equal terms. That is why all these computers are historically produced at the same factory.

Every ACM computer consists of P parts. When all these parts are present, the computer is ready and can be shipped to one of the numerous ACM contests.

Computer manufacturing is fully automated by using N various machines. Each machine removes some parts from a half-finished computer and adds some new parts (removing of parts is sometimes necessary as the parts cannot be added to a computer in arbitrary order). Each machine is described by its performance (measured in computers per hour), input and output specification.

Input specification describes which parts must be present in a half-finished computer for the machine to be able to operate on it. The specification is a set of P numbers 0, 1 or 2 (one number for each part), where 0 means that corresponding part must not be present, 1 — the part is required, 2 — presence of the part doesn’t matter.

Output specification describes the result of the operation, and is a set of P numbers 0 or 1, where 0 means that the part is absent, 1 — the part is present.

The machines are connected by very fast production lines so that delivery time is negligibly small compared to production time.

After many years of operation the overall performance of the ACM Computer Factory became insufficient for satisfying the growing contest needs. That is why ACM directorate decided to upgrade the factory.

As different machines were installed in different time periods, they were often not optimally connected to the existing factory machines. It was noted that the easiest way to upgrade the factory is to rearrange production lines. ACM directorate decided to entrust you with solving this problem.

Input 
Input file contains integers P N, then N descriptions of the machines. The description of ith machine is represented as by 2 P + 1 integers Qi Si,1 Si,2…Si,P Di,1 Di,2…Di,P, where Qi specifies performance, Si,j — input specification for part j, Di,k — output specification for part k.

Constraints

1 ≤ P ≤ 10, 1 ≤ N ≤ 50, 1 ≤ Qi ≤ 10000

Output 
Output the maximum possible overall performance, then M — number of connections that must be made, then M descriptions of the connections. Each connection between machines A and B must be described by three positive numbers A B W, where W is the number of computers delivered from A to B per hour.

If several solutions exist, output any of them.

Sample Input 
3 4 
15 0 0 0 0 1 0 
10 0 0 0 0 1 1 
30 0 1 2 1 1 1 
3 0 2 1 1 1 1 
3 5 
5 0 0 0 0 1 0 
100 0 1 0 1 0 1 
3 0 1 0 1 1 0 
1 1 0 1 1 1 0 
300 1 1 2 1 1 1 
2 2 
100 0 0 1 0 
200 0 1 1 1 
Sample Output 
25 2 
1 3 15 
2 3 10 
4 5 
1 3 3 
3 5 3 
1 2 1 
2 4 1 
4 5 1 
0 0

—————————————————–分割线——————————————————–

题意，有N个机器，每个机器对P个部分进行加工，但是每个机器对加工的对象都有要求，题中input specification 代表机器加工的对象必须满足的条件，其中为0的部分绝对不能存在，为1的部分必须存在，为2的部位存在与不存在都可以。Output specification 代表机器加工完成后的对象， 其中为0的部分代表加工后不存在，为1的部分代表加工后存在。用这些机器将全为0的零件加工成全为1的电脑。给出每个机器的加工速度，加工对象和加工后对象，求最快的加工速度。 
解释案例： 
3 4 
15 0 0 0 0 1 0 
10 0 0 0 0 1 1 
30 0 1 2 1 1 1 
3 0 2 1 1 1 1 
有四个机器，每个机器对三个地方加工。 
一开始的板子是空的，所以只能用0 0 0 开始的机器来加工，所以一开始只有1号和2号机子可以用，用1号机子后变成0 1 0 然后拿去三号机子，变成1 1 1，这一条路加工速度为15。用2号机子加工变成0 1 1，然后拿去三号机子加工，这条路加工为10，所以总的速度是25。 
思路：对于每个点先要把点分割开，把点分开成两部分的意义在于，不能让最大流量超过本身的生产量。这是因为每个点我都需要一进一出，而我自己又有自己最大的生产量，所以我要保证在网络流图上跑的时候不仅不会超过前一个点带来的流量，也不会超过自己本身所可以承受的流量。如图： 
假设c能承受的流量只有15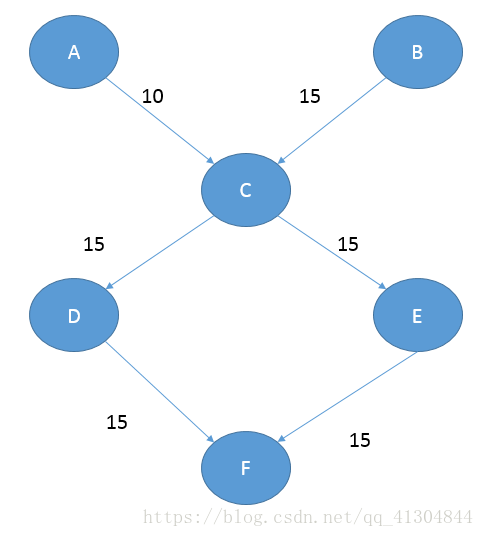 
 
如果按这个图跑，那么我会超出自身可以承受的流量，超出15，使最大流变成30，这显然是不可以的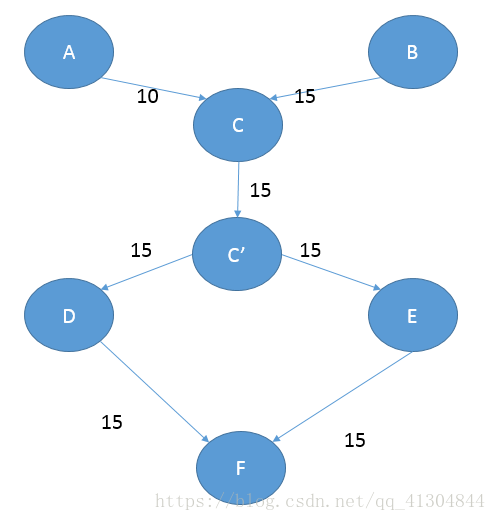 
 
那么我这时候就需要对c点进行拆点，是一条从自身到自身的路的权值是自身的生产量，这样我就保证了我不会超出自身最大可以承受的流量。 
同理，在这题中就需要对每个点来进行拆点，然后一个点用来接收流量，一个点用来发送流量，在这两个点之间用本身可以承受的最大流量来将这两个点连接起来，在这题中也就是本身的生产速度。最后跑一边最大流，然后对每条边判断，如果一开始的边比跑完以后的边的权值大，那么就说明有流量经过。

#include<map>
#include<ctime>
#include<cmath>
#include<stack>
#include<queue>
#include<string>
#include<vector>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>

typedef unsigned long long int ull;
typedef long long int ll;
const double pi = 4.0*atan(1.0);
const int inf = 0x3f3f3f3f;
const int maxn = ;
const int maxm = ;
using namespace std;

int n, m;
int maps[maxn][maxn];
int flow[maxn];
int pre[maxn];
int tmp[maxn][maxn];
int inp[maxn][maxn];
int oup[maxn][maxn];
int res[maxm][];
queue<int> q;

void init() {
    memset(inp, , sizeof(inp));
    memset(oup, , sizeof(oup));
    memset(tmp, , sizeof(tmp));
    memset(res, , sizeof(res));
    memset(maps, , sizeof(maps));
    memset(flow, , sizeof(flow));
}

void getmap() {
    int src = ;
    int des =  * m + ;
    int val;
    for(int i=; i<=m; i++) {
        scanf("%d", &val);
        maps[i][i+m] = val;
        bool flag = true;
        for(int j=; j<=n; j++) {
            scanf("%d", &inp[i][j]);
            if(inp[i][j] == )    flag = false;
        }
        if(flag)
            maps[src][i] = inf;
        flag = true;
        for(int j=; j<=n; j++) {
            scanf("%d", &oup[i][j]);
            if(oup[i][j] == )    flag = false;
        }
        if(flag)
            maps[i + m][des] = inf;
    }
    for(int i=; i<=m; i++) {
        for(int j=; j<=m; j++) {
            if(i == j)    continue;
            int flag = true;
            for(int k=; k<=n; k++) {
                if(oup[i][k] ==  && inp[j][k] == )    flag = false;
                if(oup[i][k] ==  && inp[j][k] == )    flag = false;
            }
            if(flag)
                maps[i+m][j] = inf;
        }
    }
}

int bfs(int src, int des) {
    while(!q.empty())    q.pop();
    memset(pre, -, sizeof(pre));
    q.push(src);
    pre[src] = ;
    flow[src] = inf;
    while(!q.empty()) {
        int index = q.front();
        q.pop();
        if(index == des)    break;
        for(int i=src; i<=des; i++) {
            if(i != src && maps[index][i] && pre[i] == -) {
                pre[i] = index;
                flow[i] = min(flow[index], maps[index][i]);
                q.push(i);
            }
        }
    }
    if(pre[des] == -)    return -;
    else    return flow[des];
}

int EK(int src, int des) {
    int ans = ;
    int val;
    while() {
        val = bfs(src, des);
        if(val == -)    break;
        int last = des;
        while(last != src) {
            maps[pre[last]][last] -= val;
            maps[last][pre[last]] += val;
            last = pre[last];
        }
        ans += val;
    }
    return ans;
}

int solve() {
    int ans = ;
    for(int i=; i<=m; i++) {
        for(int j=; j<=m; j++) {
            if(tmp[i + m][j] - maps[i + m][j] > ) {
                res[ans][] = i;
                res[ans][] = j;
                res[ans][] = tmp[i + m][j] - maps[i + m][j];
                ans++;
            }
        }
    }
    return ans;
}

int main() {
    while(~scanf("%d%d", &n, &m)) {
        init();
        getmap();
        int src = ;
        int des =  * m + ;
        /*
        for(int i=src; i<=des; i++) {
            for(int j=src; j<=des; j++) {
                printf("%d%c", maps[i][j], j==des ? '\n' : '\t');
            }
        }
        */
        memcpy(tmp, maps, sizeof(maps));
        int ans = EK(src, des);
        int tol = solve();
        printf("%d %d\n", ans, tol);
        for(int i=; i<tol; i++) {
            printf("%d %d %d\n", res[i][], res[i][], res[i][]);
        }
    }
    return ;
}