BZOJ4802 欧拉函数 数论

原文链接http://www.cnblogs.com/zhouzhendong/p/8117744.html

---

题目传送门 - BZOJ4802

---

题意概括

Description

已知N，求phi(N)

Input

正整数N。N<=10^18

---

题解

　　Miller_Rabin+Pollard_Rho

　　至于Pollard_Rho，我感到很奇怪。判定的时候为何不能丢第一个值！！

　　请看下面两个代码，第一个对的，第二个错的……

---

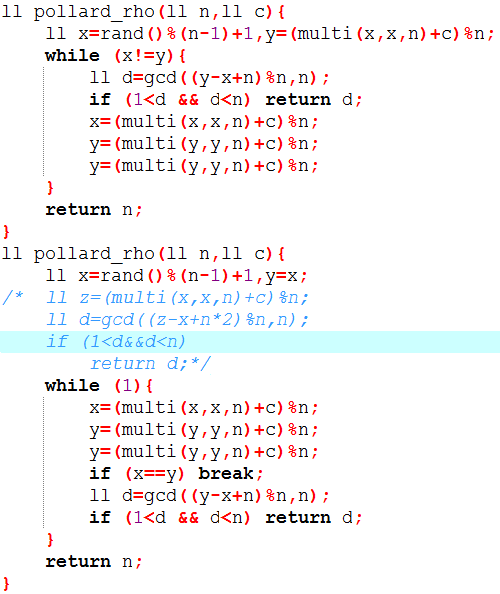
代码

#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cstdlib>
#include <cmath>
#include <ctime>
using namespace std;
typedef long long LL;
LL gcd(LL a,LL b){
	return b?gcd(b,a%b):a;
}
LL Mul(LL a,LL b,LL mod){
	LL ans=0;
	a%=mod;
	while (b){
		if (b&1)
			ans=(ans+a)%mod;
		b>>=1,a=(a<<1)%mod;
	}
	return ans;
}
LL Pow(LL a,LL b,LL mod){
	LL ans=1;
	a%=mod;
	while (b){
		if (b&1)
			ans=Mul(ans,a,mod);
		b>>=1,a=Mul(a,a,mod);
	}
	return ans;
}
bool Miller_Rabin(LL n){
	if (n==2)
		return 1;
	if (n<2||n%2==0)
		return 0;
	LL m=n-1,k=0;
	while (!(m&1))
		m>>=1,k++;
	for (int i=0;i<10;i++){
		LL a=rand()%(n-1)+1,x=Pow(a,m,n),y;
		for (int j=0;j<k;j++){
			y=Mul(x,x,n);
			if (y==1&&x!=1&&x!=n-1)
				return 0;
			x=y;
		}
		if (x!=1)
			return 0;
	}
	return 1;
}
LL rnd(LL x,LL n,LL c){
	return (Mul(x,x,n)+c)%n;
}
LL Pollard_Rho(LL n,LL c){
	LL x,y;
	while (1){
		x=rand()%(n-1)+1,y=rnd(x,n,c);
		while (1){
			if (x==y)
				break;
			LL d=gcd(llabs(y-x)%n,n);
			if (1<d&&d<n)
				return d;
			x=rnd(x,n,c);
			y=rnd(rnd(y,n,c),n,c);
		}
		c=rand()%n;
	}
}
LL n,x[66],pcnt;
void find(LL n){
	if (n==1)
		return;
	if (Miller_Rabin(n)){
		x[++pcnt]=n;
		return;
	}
	LL p=Pollard_Rho(n,rand()%n);
	find(p);
	find(n/p);
}
int main(){
	srand(19260817);
	scanf("%lld",&n);
	pcnt=0;
	find(n);
	sort(x+1,x+pcnt+1);
	LL yz=pcnt?x[1]-1:1;
	for (int i=2;i<=pcnt;i++)
		yz=yz*(x[i]-(bool)(x[i]!=x[i-1]));
	printf("%lld\n",yz);
	return 0;
}